97视频网站,九色在线观看,久久久成人av

精英家教網 > 高中數學 > 題目詳情

【題目】極坐標系與直角坐標系xoy有相同的長度單位，以原點O為極點，以x軸正半軸為極軸．已知直線l的參數方程為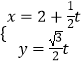（t為參數），曲線C的極坐標方程為ρsin2θ=8cosθ．（I）求C的直角坐標方程；
（Ⅱ）設直線l與曲線C交于A，B兩點，求弦長|AB|．

【答案】解：（I）由曲線C的極坐標方程為ρsin2θ=8cosθ，即ρ2sin2θ=8ρcosθ，化為y2=8x．（II）把直線l的參數方程為（t為參數）代入y2=8x化為3t2﹣16t﹣64=0．
解得t1=8，t2= ．
∴弦長|AB|=|t1﹣t2|= =
【解析】（I）利用即可得出直角坐標方程．（II）把直線l的參數方程為（t為參數）代入y2=8x化為3t2﹣16t﹣64=0．利用弦長|AB|=|t1﹣t2|即可得出．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】已知非空集合A，B滿足以下兩個條件．
（ⅰ）A∪B={1，2，3，4，5，6}，A∩B=；
（ⅱ）A的元素個數不是A中的元素，B的元素個數不是B中的元素，則有序集合對（A，B）的個數為（）
A.10
B.12
C.14
D.16

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，平行四邊形ABCD中，CD=1，∠BCD=60°，BD⊥CD，正方形ADEF，且面ADEF⊥面ABCD．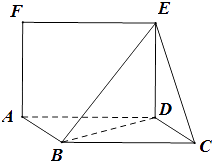
（Ⅰ）求證：BD⊥平面ECD．
（Ⅱ）求D點到面CEB的距離．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】有下列說法： ①函數y=﹣cos2x的最小正周期是π；
②終邊在y軸上的角的集合是{α|α= ，k∈Z}；
③在同一直角坐標系中，函數y=sinx的圖象和函數y=x的圖象有三個公共點；
④函數f（x）=4sin（2x+ ）（x∈R）可以改寫為y=4cos（2x﹣ ）；
⑤函數y=sin（x﹣ ）在[0，π]上是減函數．
其中，正確的說法是．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某工廠生產一種機器的固定成本為5000元，且每生產100部，需要加大投入2500元．對銷售市場進行調查后得知，市場對此產品的需求量為每年500部，已知銷售收入函數為，其中x是產品售出的數量0≤x≤500．
（1）若為x年產量，y表示利潤，求y=f（x）的解析式
（2）當年產量為何值時，工廠的年利潤最大？其最大值是多少？