
【題目】已知![]() 分別是直線
分別是直線![]() 和
和![]() 上的兩個動點,線段
上的兩個動點,線段![]() 的長為
的長為![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若過點(1,0)的直線![]() 與曲線
與曲線![]() 交于不同兩點
交于不同兩點![]() .
.
①當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
②試問在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 恒為定值?若存在,求出
恒為定值?若存在,求出![]() 點的坐標及定值;若不存在,請說明理由.
點的坐標及定值;若不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)① ![]() 或
或![]() ;②存在,點
;②存在,點![]() ,
,![]() .
.
【解析】
試題分析:(1)本問考查求軌跡方程的直接法,即根據題中已知條件,轉化為關于定點的坐標表示,首先設點![]() ,
,![]() ,
,![]() ,根據中點坐標公式有
,根據中點坐標公式有![]() ,
,![]() ,再根據兩點間距離公式表示出線段
,再根據兩點間距離公式表示出線段![]() 的長度,于是可以整理得到關于點
的長度,于是可以整理得到關于點![]() 的方程,即為所求軌跡
的方程,即為所求軌跡![]() ;(2)①本問主要考查直線與圓相交,有關弦長問題,可以根據垂徑定理進行求解,注意對直線
;(2)①本問主要考查直線與圓相交,有關弦長問題,可以根據垂徑定理進行求解,注意對直線![]() 的斜率是否存在進行討論;②本問主要考查解析幾何中直線與圓的問題,首先假設存在點
的斜率是否存在進行討論;②本問主要考查解析幾何中直線與圓的問題,首先假設存在點![]() 使得
使得![]() 為定值,把直線方程與圓的方程聯立,消去未知數
為定值,把直線方程與圓的方程聯立,消去未知數![]() ,得到關于
,得到關于![]() 的一元二次方程,設點
的一元二次方程,設點![]() ,
,![]() ,表示出
,表示出![]() ,
,![]() 的值,然后將
的值,然后將![]() 用坐標表示出來,得到關于
用坐標表示出來,得到關于![]() 的表達式,若
的表達式,若![]() 為定值,則分母應為分子的倍數,可以采用待定系數法求解.
為定值,則分母應為分子的倍數,可以采用待定系數法求解.
試題解析:(1)設點![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
又根據題意![]() ①,
①,![]() ②,且
②,且![]() ,
,
所以由①②得:![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以動點![]() 的軌跡
的軌跡![]() 的方程為:
的方程為:![]() ;
;
(2)①當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() ,經計算,此時
,經計算,此時![]() ,不符合題意;
,不符合題意;
當直線![]() 的斜率存在時,設方程為
的斜率存在時,設方程為![]() ,圓心到直線
,圓心到直線![]() 的距離
的距離![]() ,
,
根據垂徑定理![]() 有:
有:![]() ,
,
解得![]() ,所以
,所以![]() ,
,
所以直線![]() 的方程為
的方程為![]() 或
或![]() ;
;
②假設存在點![]() 使得
使得![]() 為定值,
為定值,
當直線![]() 的斜率存在時,設方程為
的斜率存在時,設方程為![]() ,
,
由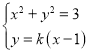 消去
消去![]() 得:
得:![]() ,
,
易知![]() 成立,設點
成立,設點![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
若![]() 為定值,則必有
為定值,則必有![]() ,解得
,解得![]() ,點
,點![]() ,
,
所以![]() ,
,
當直線![]() 斜率不存在時,方程為
斜率不存在時,方程為![]() ,此時
,此時![]() ,
,![]() ,此時
,此時![]() ,
,
綜上所述,當點![]() 時,
時,![]() 為定值
為定值![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像是由函數
的圖像是由函數![]() 的圖像經如下變換得到:先將
的圖像經如下變換得到:先將![]() 圖像上所有點的縱坐標伸長到原來的2倍(橫坐標不變),再將所得到的圖像向右平移
圖像上所有點的縱坐標伸長到原來的2倍(橫坐標不變),再將所得到的圖像向右平移![]() 個單位長度.
個單位長度.
(Ⅰ)求函數![]() 的解析式,并求其圖像的對稱軸方程;
的解析式,并求其圖像的對稱軸方程;
(Ⅱ)已知關于![]() 的方程
的方程![]() 在
在![]() 內有兩個不同的解
內有兩個不同的解![]() .
.
(1)求實數m的取值范圍;
(2)證明:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三次函數![]() ,下列命題正確的是 .
,下列命題正確的是 .
①函數![]() 關于原點
關于原點![]() 中心對稱;
中心對稱;
②以![]() ,
,![]() 兩不同的點為切點作兩條互相平行的切線,分別與
兩不同的點為切點作兩條互相平行的切線,分別與![]() 交于
交于![]() 兩點,則這四個點的橫坐標滿足關系
兩點,則這四個點的橫坐標滿足關系![]() ;
;
③以![]() 為切點,作切線與
為切點,作切線與![]() 圖像交于點
圖像交于點![]() ,再以點
,再以點![]() 為切點作直線與
為切點作直線與![]() 圖像交于點
圖像交于點![]() ,再以點
,再以點![]() 作切點作直線與
作切點作直線與![]() 圖像交于點
圖像交于點![]() ,則
,則![]() 點橫坐標為
點橫坐標為![]() ;
;
④若![]() ,函數
,函數![]() 圖像上存在四點
圖像上存在四點![]() ,使得以它們為頂點的四邊形有且僅有一個正方形.
,使得以它們為頂點的四邊形有且僅有一個正方形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶假期是實施免收小型客車高速通行費的重大節假日,有一個群名為“天狼星”的自駕游車隊,該車隊是由31輛身長約為![]() (以
(以![]() 計算)的同一車型組成,行程中經過一個長為2725
計算)的同一車型組成,行程中經過一個長為2725![]() 的隧道(通過隧道的車速不超過
的隧道(通過隧道的車速不超過![]() ),勻速通過該隧道,設車隊的速度為
),勻速通過該隧道,設車隊的速度為![]() ,根據安全和車流的需要,當
,根據安全和車流的需要,當![]() 時,相鄰兩車之間保持
時,相鄰兩車之間保持![]() 的距離;當
的距離;當![]() 時,相鄰兩車之間保持
時,相鄰兩車之間保持![]() 的距離,自第一輛車車頭進入隧道至第31輛車車尾離開隧道所用的時間
的距離,自第一輛車車頭進入隧道至第31輛車車尾離開隧道所用的時間![]() .
.
(1)將![]() 表示成為
表示成為![]() 的函數;
的函數;
(2)求該車隊通過隧道時間![]() 的最小值及此時車隊的速度.
的最小值及此時車隊的速度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() ),且數列
),且數列![]() 是首項為2,公差為2的等差數列.
是首項為2,公差為2的等差數列.
(1)若![]() ,當
,當![]() 時,求數列
時,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(2)設![]() ,如果
,如果![]() 中的每一項恒小于它后面的項,求
中的每一項恒小于它后面的項,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在![]() 軸正半軸上的圓
軸正半軸上的圓![]() 與直線
與直線![]() 相切,與
相切,與![]() 軸交于
軸交于![]() 兩點,且
兩點,且![]() .
.
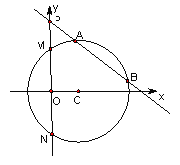
(1)求圓![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,若設點
,若設點![]() 為
為![]() 的重心,當
的重心,當![]() 的面積為
的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com