
【題目】已知函數(shù)![]() .
.
(1)當(dāng)函數(shù)![]() 與函數(shù)
與函數(shù)![]() 圖象的公切線l經(jīng)過坐標(biāo)原點時,求實數(shù)a的取值集合;
圖象的公切線l經(jīng)過坐標(biāo)原點時,求實數(shù)a的取值集合;
(2)證明:當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有兩個零點
有兩個零點![]() ,且滿足
,且滿足![]() .
.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)先利用導(dǎo)數(shù)的幾何意義和函數(shù)![]() 求出公切線方程,再將公切線方程與函數(shù)
求出公切線方程,再將公切線方程與函數(shù)![]() 聯(lián)立,表示
聯(lián)立,表示![]() ,再構(gòu)造函數(shù)
,再構(gòu)造函數(shù)![]() 利用導(dǎo)數(shù)求出其單調(diào)區(qū)間和值域,可求出a的取值;
利用導(dǎo)數(shù)求出其單調(diào)區(qū)間和值域,可求出a的取值;
(2)要證![]() 有兩個零點,只要證
有兩個零點,只要證![]() 有兩個零點即可,而
有兩個零點即可,而![]() 時函數(shù)
時函數(shù)![]() 的一個零點,所以只需再利用導(dǎo)數(shù)研究此函數(shù)的性質(zhì)即可,由于兩個零點,一個是
的一個零點,所以只需再利用導(dǎo)數(shù)研究此函數(shù)的性質(zhì)即可,由于兩個零點,一個是![]() ,另一個在區(qū)間
,另一個在區(qū)間![]() 上,若設(shè)
上,若設(shè)![]() 則
則![]() , 所以只需利用導(dǎo)數(shù)證明
, 所以只需利用導(dǎo)數(shù)證明![]() 即可 .
即可 .
解:(1)設(shè)公切線l與函數(shù)![]() 的切點為
的切點為![]() ,則公切線l的斜率
,則公切線l的斜率![]() ,公切線l的方程為:
,公切線l的方程為:![]() ,將原點坐標(biāo)
,將原點坐標(biāo)![]() 代入,得
代入,得![]() ,解得
,解得![]() ,公切線l的方程為:
,公切線l的方程為:![]() ,
,
將它與![]() 聯(lián)立,整理得
聯(lián)立,整理得![]() .
.
令![]() ,對之求導(dǎo)得:
,對之求導(dǎo)得:![]() ,令
,令![]() ,解得
,解得![]() .
.
當(dāng)![]() 時,
時,![]() 單調(diào)遞減,值域為
單調(diào)遞減,值域為![]() ,
,
當(dāng)![]() 時,
時,![]() 單調(diào)遞增,值域為
單調(diào)遞增,值域為![]() ,
,
由于直線l與函數(shù)![]() 相切,即只有一個公共點,
相切,即只有一個公共點,
故實數(shù)a的取值集合為![]() .
.
(2)證明:![]() ,要證
,要證![]() 有兩個零點,只要證
有兩個零點,只要證![]() 有兩個零點即可.
有兩個零點即可.![]() ,即
,即![]() 時函數(shù)
時函數(shù)![]() 的一個零點.
的一個零點.
對![]() 求導(dǎo)得:
求導(dǎo)得:![]() ,令
,令![]() ,解得
,解得![]() .當(dāng)
.當(dāng)![]() 時,
時,![]() 單調(diào)遞增;
單調(diào)遞增;
當(dāng)![]() 時,
時,![]() 單調(diào)遞減.當(dāng)
單調(diào)遞減.當(dāng)![]() 時,
時,![]() 取最小值,
取最小值,![]() ,
,![]() ,必定存
,必定存![]() 在使得二次函數(shù)
在使得二次函數(shù)![]() ,
,
即![]() .因此在區(qū)間上
.因此在區(qū)間上![]() 必定存在
必定存在![]() 的一個零點.
的一個零點.
練上所述,![]() 有兩個零點,一個是
有兩個零點,一個是![]() ,另一個在區(qū)間
,另一個在區(qū)間![]() 上.
上.
下面證明![]() .
.
由上面步驟知![]() 有兩個零點,一個是
有兩個零點,一個是![]() ,另一個在區(qū)間
,另一個在區(qū)間![]() 上.
上.
不妨設(shè)![]() 則
則![]() ,下面證明
,下面證明![]() 即可.
即可.
令![]() ,對之求導(dǎo)得
,對之求導(dǎo)得![]() ,
,
故![]() 在定義域內(nèi)單調(diào)遞減,
在定義域內(nèi)單調(diào)遞減,![]() ,即
,即![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉(zhuǎn)成
翻轉(zhuǎn)成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分別為線段
分別為線段![]() 的中點,則在
的中點,則在![]() 翻轉(zhuǎn)過程中,下列說法正確的是( )
翻轉(zhuǎn)過程中,下列說法正確的是( )
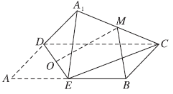
A.與平面![]() 垂直的直線必與直線
垂直的直線必與直線![]() 垂直
垂直
B.異面直線![]() 與
與![]() 所成的角是定值
所成的角是定值
C.一定存在某個位置,使![]()
D.三棱錐![]() 外接球半徑與棱
外接球半徑與棱![]() 的長之比為定值
的長之比為定值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知多面體![]() ,其底面
,其底面![]() 為矩形,四邊形
為矩形,四邊形![]() 為平行四邊形,平面
為平行四邊形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
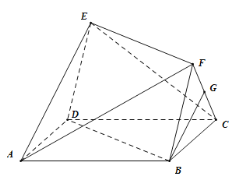
(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義域均為D的三個函數(shù)![]() ,
,![]() ,
,![]() 滿足條件:對任意
滿足條件:對任意![]() ,點
,點![]() 與點
與點![]() 都關(guān)于點
都關(guān)于點![]() 對稱,則稱
對稱,則稱![]() 是
是![]() 關(guān)于
關(guān)于![]() 的“對稱函數(shù)”.已知函數(shù)
的“對稱函數(shù)”.已知函數(shù)![]() ,
,![]() ,
,![]() 是
是![]() 關(guān)于
關(guān)于![]() 的“對稱函數(shù)“,記
的“對稱函數(shù)“,記![]() 的定義域為D,若對任意
的定義域為D,若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,則實數(shù)a的取值范圍是( )
成立,則實數(shù)a的取值范圍是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
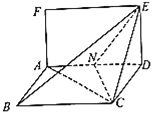
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() 的中點.
的中點.
(Ⅰ)試問在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?若存在,請證明
?若存在,請證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“二進制”來源于我國古代的《易經(jīng)》,該書中有兩類最基本的符號:“─”和“﹣﹣”,其中“─”在二進制中記作“1”,“﹣﹣”在二進制中記作“0”.如符號“”對應(yīng)的二進制數(shù)011(2)化為十進制的計算如下:011(2)=0×22+1×21+1×20=3(10).若從兩類符號中任取2個符號進行排列,則得到的二進制數(shù)所對應(yīng)的十進制數(shù)大于2的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】受新冠肺炎疫情影響,某學(xué)校按上級文件指示,要求錯峰放學(xué),錯峰有序吃飯.高三年級一層樓六個班排隊,甲班必須排在前三位,且丙班、丁班必須排在一起,則這六個班排隊吃飯的不同安排方案共有( )
A.240種B.120種C.188種D.156種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)不需證明,直接寫出![]() 的奇偶性:
的奇偶性:
(Ⅱ)討論![]() 的單調(diào)性,并證明
的單調(diào)性,并證明![]() 有且僅有兩個零點:
有且僅有兩個零點:
(Ⅲ)設(shè)![]() 是
是![]() 的一個零點,證明曲線
的一個零點,證明曲線![]() 在點
在點![]() 處的切線也是曲線
處的切線也是曲線![]() 的切線.
的切線.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com