
【題目】如圖,在矩形![]() 中,
中,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分別為線段
分別為線段![]() 的中點,則在
的中點,則在![]() 翻轉過程中,下列說法正確的是( )
翻轉過程中,下列說法正確的是( )
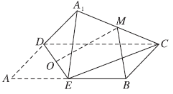
A.與平面![]() 垂直的直線必與直線
垂直的直線必與直線![]() 垂直
垂直
B.異面直線![]() 與
與![]() 所成的角是定值
所成的角是定值
C.一定存在某個位置,使![]()
D.三棱錐![]() 外接球半徑與棱
外接球半徑與棱![]() 的長之比為定值
的長之比為定值
科目:高中數學 來源: 題型:
【題目】某人堅持跑步鍛煉,根據他最近20周的跑步數據,制成如下條形圖:
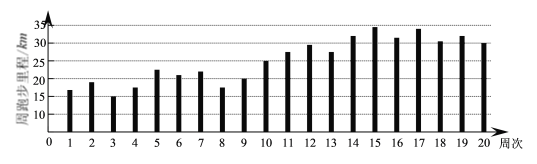
根據條形圖判斷,下列結論正確的是( )
A.周跑步里程逐漸增加
B.這20周跑步里程平均數大于30km
C.這20周跑步里程中位數大于30km
D.前10周的周跑步里程的極差大于后10周的周跑步里程的極差
查看答案和解析>>
科目:高中數學 來源: 題型:
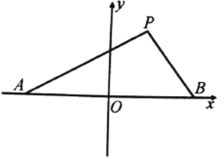
【題目】如圖,設點![]() 的坐標分別為
的坐標分別為![]() ,直線
,直線![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為
的軌跡為![]() ,點
,點![]() 是軌跡為
是軌跡為![]() 上不同于
上不同于![]() 的兩點,且滿足
的兩點,且滿足![]() ,求證:
,求證:![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四面體![]() 中,棱
中,棱![]() ,
,![]() 所在直線所成角為
所在直線所成角為![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,當四面體
,當四面體![]() 的體積取得最大值時( ).
的體積取得最大值時( ).
A.![]() B.
B.![]() C.
C.![]() D.不能確定
D.不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是拋物線
是拋物線![]() 上的兩個不同的點,
上的兩個不同的點,![]() 是坐標原點.若直線
是坐標原點.若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,則( ).
,則( ).
A.![]() B.以
B.以![]() 為直徑的圓的面積大于
為直徑的圓的面積大于![]()
C.直線![]() 過定點
過定點![]() D.點
D.點![]() 到直線
到直線![]() 的距離不大于2
的距離不大于2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年4月8日,武漢市雷神山醫院為確診新型冠狀病毒肺炎患者,需要檢測核酸是否為陽性,現有![]() 份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測
份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測![]() 次;(2)混合檢測,將其中
次;(2)混合檢測,將其中![]() (
(![]() ,且
,且![]() )份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這
)份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這![]() 份核酸樣本全為陰性,因而這
份核酸樣本全為陰性,因而這![]() 份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這
份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這![]() 份核酸樣本究竟哪幾份為陽性,就要對這
份核酸樣本究竟哪幾份為陽性,就要對這![]() 份樣本再逐份檢測,此時這
份樣本再逐份檢測,此時這![]() 份核酸樣本的檢測次數總共為
份核酸樣本的檢測次數總共為![]() 次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份核酸樣本,其中只有2份樣本為陽性,若采用逐份檢測方式,求恰好經過4次檢測就能把陽性樣本全部檢測出來的概率.
(2)現取其中![]() (
(![]() ,且
,且![]() )份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為
)份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為![]() ,采用混合檢測方式,樣本需要檢測的總次數為
,采用混合檢測方式,樣本需要檢測的總次數為![]() .
.
①試運用概率統計的知識,若![]() ,試求
,試求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
②若![]() ,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求
,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求![]() 的最大值.
的最大值.
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】法國數學家龐加是個喜歡吃面包的人,他每天都會購買一個面包,面包師聲稱自己出售的每個面包的平均質量是1000![]() ,上下浮動不超過50
,上下浮動不超過50![]() .這句話用數學語言來表達就是:每個面包的質量服從期望為1000
.這句話用數學語言來表達就是:每個面包的質量服從期望為1000![]() ,標準差為50
,標準差為50![]() 的正態分布.
的正態分布.
(1)假設面包師的說法是真實的,從面包師出售的面包中任取兩個,記取出的兩個面包中質量大于1000![]() 的個數為
的個數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)作為一個善于思考的數學家,龐加萊每天都會將買來的面包稱重并記錄,25天后,得到數據如下表,經計算25個面包總質量為24468![]() .龐加萊購買的25個面包質量的統計數據(單位:
.龐加萊購買的25個面包質量的統計數據(單位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
盡管上述數據都落在![]() 上,但龐加菜還是認為面包師撒謊,根據所附信息,從概率角度說明理由
上,但龐加菜還是認為面包師撒謊,根據所附信息,從概率角度說明理由
附:
①若![]() ,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則由統計學知識可知:隨機變量
,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則由統計學知識可知:隨機變量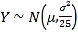
②若![]() ,則
,則![]() ,
,![]() ,
,![]() ;
;
③通常把發生概率在0.05以下的事件稱為小概率事件.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com