
【題目】如圖,在多邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是線段
是線段![]() 上的一點,且
上的一點,且![]() ,若將
,若將![]() 沿
沿![]() 折起,得到幾何體
折起,得到幾何體![]() .
.
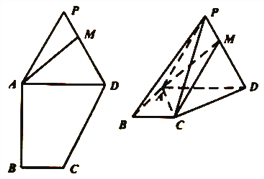
(1)試問:直線![]() 與平面
與平面![]() 是否有公共點?并說明理由;
是否有公共點?并說明理由;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】如圖,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如圖,以C為原點,分別以CA,CB,CC1為x,y,z軸建立空間直角坐標系.
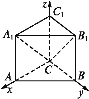
(1)求平面A1B1C的法向量;
(2)求直線AC與平面A1B1C夾角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列命題:(1)終邊相同的角的同名三角比的值相等;(2)終邊不同的角的同名三角比的值不同;(3)若![]() ,則
,則![]() 是第一或第二象限角;(4)△
是第一或第二象限角;(4)△![]() 中,若
中,若![]() ,則
,則![]() ;其中正確命題的個數是( )
;其中正確命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】進入12月以來,某地區為了防止出現重污染天氣,堅持保民生、保藍天,嚴格落實機動車限行等一系列“管控令”.該地區交通管理部門為了了解市民對“單雙號限行”的贊同情況,隨機采訪了220名市民,將他們的意見和是否擁有私家車情況進行了統計,得到如下的![]() 列聯表:
列聯表:
贊同限行 | 不贊同限行 | 合計 | |
沒有私家車 | 90 | 20 | 110 |
有私家車 | 70 | 40 | 110 |
合計 | 160 | 60 | 220 |
(1)根據上面的列聯表判斷,能否在犯錯誤的概率不超過0.001的前提下認為“是否贊同限行與是否擁有私家車”有關;
(2)為了了解限行之后是否對交通擁堵、環境污染起到改善作用,從上述調查的不贊同限行的人員中按分層抽樣抽取6人,再從這6人中隨機抽出3名進行電話回訪,求3人中至少抽到1名“沒有私家車”人員的概率.
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點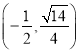 ,且離心率為
,且離心率為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若點![]() 為橢圓
為橢圓![]() 的右頂點,探究:
的右頂點,探究: ![]() 是否為定值,若是,求出該定值,若不是,請說明理由.(其中,
是否為定值,若是,求出該定值,若不是,請說明理由.(其中, ![]() ,
, ![]() 分別是直線
分別是直線![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com