
甲、乙、丙三人參加某次招聘會,假設甲能被聘用的概率是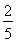 ,甲、丙兩人同時不能被聘用的概率是
,甲、丙兩人同時不能被聘用的概率是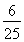 ,乙、丙兩人同時能被聘用的概率為
,乙、丙兩人同時能被聘用的概率為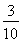 ,且三人各自能否被聘用相互獨立.
,且三人各自能否被聘用相互獨立.
(1)求乙、丙兩人各自被聘用的概率;
(2)設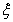 為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求
為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求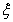 的分布列與均值(數學期望).
的分布列與均值(數學期望).
(1)乙、丙兩人各自被聘用的概率分別為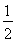 、
、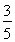 ;(2)詳見解析.
;(2)詳見解析.
【解析】
試題分析:(1)分別設乙、丙兩人各自被聘用的概率為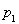 、
、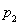 ,利用事件的獨立性列出相應的方程進行求解,從而得出乙、丙兩人各自被聘用的概率;(2)先列舉出隨機變量
,利用事件的獨立性列出相應的方程進行求解,從而得出乙、丙兩人各自被聘用的概率;(2)先列舉出隨機變量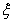 的可能取值,并根據事件的獨立性求出
的可能取值,并根據事件的獨立性求出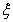 在相應條件的概率,列出分布列并求出隨機變量
在相應條件的概率,列出分布列并求出隨機變量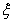 的均值(即數學期望).
的均值(即數學期望).
試題解析:(1)設乙、丙兩人各自被聘用的概率分別為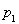 、
、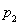 ,
,
則甲、丙兩人同時不能被聘用的概率是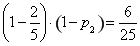 ,解得
,解得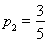 ,
,
乙、丙兩人同時能被聘用的概率為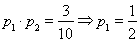 ,
,
因此乙、丙兩人各自被聘用的概率分別為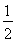 、
、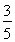 ;
;
(2)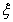 的可能取值有
的可能取值有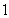 、
、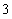 ,
,
則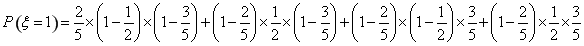
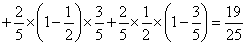 ,
,
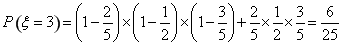 ,
,
因此隨機變量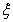 的分布列如下表所示
的分布列如下表所示
|
|
|
|
|
|
所以隨機變量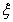 的均值(即數學期望)
的均值(即數學期望)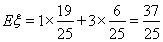 .
.
考點:1.獨立事件概率的計算;2.離散型隨機變量的概率分布列與數學期望


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十三第十章第十節練習卷(解析版) 題型:選擇題
下面是2×2列聯表:
| y1 | y2 | 總計 |
x1 | a | 21 | 73 |
x2 | 22 | 25 | 47 |
總計 | b | 46 | 120 |
則表中a,b的值分別為( )
(A)94,72 (B)52,50
(C)52,74 (D)74,52
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數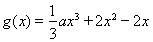 ,函數
,函數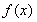 是函數
是函數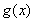 的導函數.
的導函數.
(1)若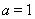 ,求
,求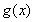 的單調減區間;
的單調減區間;
(2)若對任意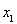 ,
,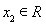 且
且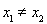 ,都有
,都有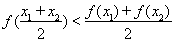 ,求實數
,求實數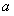 的取值范圍;
的取值范圍;
(3)在第(2)問求出的實數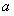 的范圍內,若存在一個與
的范圍內,若存在一個與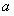 有關的負數
有關的負數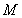 ,使得對任意
,使得對任意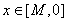 時
時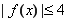 恒成立,求
恒成立,求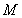 的最小值及相應的
的最小值及相應的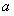 值.
值.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖,輸入的N=2014,則輸出的S=( )
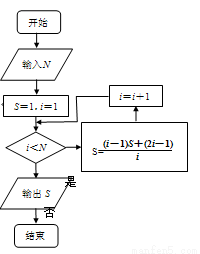
A.2011 B.2012 C.2013 D.2014
查看答案和解析>>
科目:高中數學 來源:2014年廣東省廣州市畢業班綜合測試一理科數學試卷(解析版) 題型:選擇題
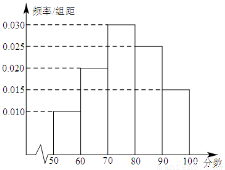
某中學從某次考試成績中抽取若干名學生的分數,并繪制成如圖所示的頻率分布直方圖,樣本數據分組為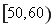 、
、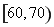 、
、 、
、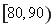 、
、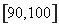 .若用分層抽樣的方法從樣本中抽取分數在
.若用分層抽樣的方法從樣本中抽取分數在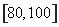 范圍內的數據
范圍內的數據 個,則其中分數在
個,則其中分數在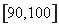 范圍內的樣本數據有( )
范圍內的樣本數據有( )
A.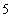 個 B.
個 B.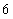 個 C.
個 C.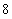 個 D.
個 D.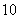 個
個
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)仿真模擬卷1練習卷(解析版) 題型:選擇題
已知雙曲線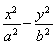 =1(a>0,b>0)的左、右焦點分別為F1,F2,點O為雙曲線的中心,點P在雙曲線右支上,△PF1F2內切圓的圓心為Q,圓Q與x軸相切于點A,過F2作直線PQ的垂線,垂足為B,則下列結論成立的是( )
=1(a>0,b>0)的左、右焦點分別為F1,F2,點O為雙曲線的中心,點P在雙曲線右支上,△PF1F2內切圓的圓心為Q,圓Q與x軸相切于點A,過F2作直線PQ的垂線,垂足為B,則下列結論成立的是( )
A.|OA|>|OB| B.|OA|<|OB|
C.|OA|=|OB| D.|OA|與|OB|大小關系不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com