
據環保部門測定,某處的污染指數與附近污染源的強度成正比,與到污染源距離的平方成反比,比例常數為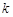
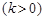 .現已知相距18
.現已知相距18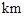 的A,B兩家化工廠(污染源)的污染強度分別為
的A,B兩家化工廠(污染源)的污染強度分別為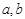 ,它們連線上任意一點C處的污染指數
,它們連線上任意一點C處的污染指數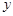 等于兩化工廠對該處的污染指數之和.設
等于兩化工廠對該處的污染指數之和.設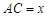 (
(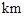 ).
).
(1)試將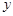 表示為
表示為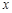 的函數; (2)若
的函數; (2)若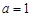 ,且
,且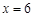 時,
時,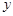 取得最小值,試求
取得最小值,試求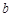 的值.
的值.
(1) 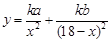 , (2) 8.
, (2) 8.
解析試題分析:(1)解實際問題應用題,關鍵要正確理解題意,正確列出等量關系,注意考慮函數定義域. 設點C受A污染源污染程度為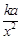 ,點C受B污染源污染程度為
,點C受B污染源污染程度為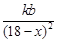 ,其中
,其中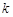 為比例系數,且
為比例系數,且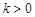 .從而點C處受污染程度
.從而點C處受污染程度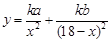 .定義域為
.定義域為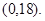 (2) 因為
(2) 因為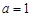 ,所以,
,所以,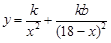 ,求復雜分式函數最值,通常考慮利用導數求解.
,求復雜分式函數最值,通常考慮利用導數求解. 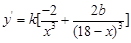 ,令
,令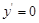 ,得
,得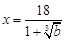 ,因此函數在
,因此函數在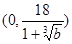 單調減,在
單調減,在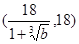 單調增,即在
單調增,即在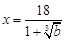 時函數取極小值,也是最小值. 又此時
時函數取極小值,也是最小值. 又此時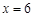 ,解得
,解得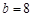 ,經驗證符合題意.
,經驗證符合題意.
解:(1)設點C受A污染源污染程度為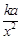 ,點C受B污染源污染程度為
,點C受B污染源污染程度為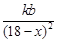 ,其中
,其中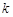 為比例系數,且
為比例系數,且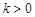 . 4分
. 4分
從而點C處受污染程度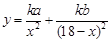 . 6分
. 6分
(2)因為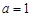 ,所以,
,所以,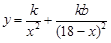 , 8分
, 8分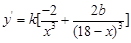 ,令
,令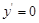 ,得
,得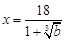 , 12分
, 12分
又此時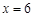 ,解得
,解得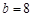 ,經驗證符合題意.
,經驗證符合題意.
所以,污染源B的污染強度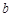 的值為8. 14分
的值為8. 14分
考點:利用導數求函數值域


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知函數 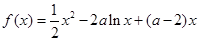 ,
,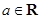 .
.
(1)當 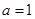 時,求函數
時,求函數 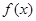 的最小值;
的最小值;
(2)當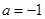 時,求證:無論
時,求證:無論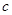 取何值,直線
取何值,直線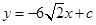 均不可能與函數
均不可能與函數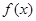 相切;
相切;
(3)是否存在實數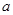 ,對任意的
,對任意的 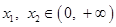 ,且
,且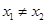 ,有
,有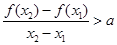 恒成立,若存在求出
恒成立,若存在求出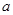 的取值范圍,若不存在,說明理由。
的取值范圍,若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•浙江)已知a∈R,函數f(x)=2x3﹣3(a+1)x2+6ax
(Ⅰ)若a=1,求曲線y=f(x)在點(2,f(2))處的切線方程;
(Ⅱ)若|a|>1,求f(x)在閉區間[0,|2a|]上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=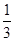 x3-ax+1.
x3-ax+1.
(1)求x=1時,f(x)取得極值,求a的值;
(2)求f(x)在[0,1]上的最小值;
(3)若對任意m∈R,直線y=-x+m都不是曲線y=f(x)的切線,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數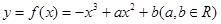
(1)若函數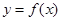 的圖象切x軸于點(2,0),求a、b的值;
的圖象切x軸于點(2,0),求a、b的值;
(2)設函數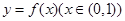 的圖象上任意一點的切線斜率為k,試求
的圖象上任意一點的切線斜率為k,試求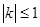 的充要條件;
的充要條件;
(3)若函數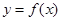 的圖象上任意不同的兩點的連線的斜率小于l,求證
的圖象上任意不同的兩點的連線的斜率小于l,求證 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com