
已知函數f(x)=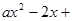 1 .
1 .
(1)試討論函數f(x)的單調性;
(2)若 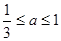 ,且f(x)在區間[1,3]上的最大值為M(a) ,最小值為N(a),
,且f(x)在區間[1,3]上的最大值為M(a) ,最小值為N(a),
令g(a)= M(a)-N(a),求 g(a)的表達式,試求g(a)的最小值.
(1)a=0,y=f(x)在R上單調遞減
a>0時,對稱軸是x=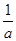 ,
增區間
,
增區間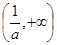 ,減區間是
,減區間是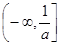
a<0時,對稱軸是x=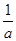 ,
增區間
,
增區間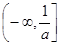 ,減區間是
,減區間是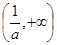
(2)g(a)=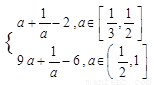 ,易得 g(a)最小值是
,易得 g(a)最小值是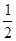
【解析】本試題主要是考查了含有參數二次函數的單調性和函數的最值的問題的運用。
(1)對參數a分類討論,得到不同性質的函數,分析其單調性。
(2)因為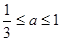 ,且f(x)在區間[1,3]上的最大值為M(a) ,最小值為N(a),結合上一問的結論得到最值,然后令g(a)= M(a)-N(a),整體來分析新函數的最值即可。
,且f(x)在區間[1,3]上的最大值為M(a) ,最小值為N(a),結合上一問的結論得到最值,然后令g(a)= M(a)-N(a),整體來分析新函數的最值即可。
(1)a=0,y=f(x)在R上單調遞減
a>0時,對稱軸是x=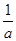 ,
增區間
,
增區間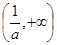 ,減區間是
,減區間是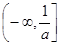
a<0時,對稱軸是x=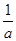 ,
增區間
,
增區間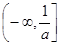 ,減區間是
,減區間是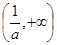
(2) 當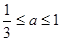 ,1≤
,1≤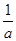 ≤3,N(a)=f(
≤3,N(a)=f(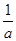 )=1-
)=1-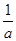 ,
,
當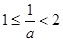 ,即
,即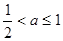 時,M(a)=f(3)=9a-5,所以g(a)=9a+
時,M(a)=f(3)=9a-5,所以g(a)=9a+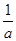 -6
-6
當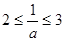 ,即
,即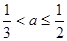 時,M(a)=f(1)=a-1,所以g(a)=a+
時,M(a)=f(1)=a-1,所以g(a)=a+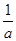 -2
-2
綜上g(a)=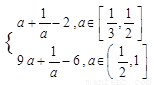 ,易得 g(a)最小值是
,易得 g(a)最小值是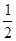


科目:高中數學 來源: 題型:
1+
| ||||
sin(x+
|
| 3 |
| 5 |
| 3 |
| m |
| π |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1+lnx |
| x |
| 1 |
| 2 |
| k |
| x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 1 | ||
|
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1-m•2x | 1+m•2x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com