
【題目】已知函數![]() .
.
(1)當![]() 時,判斷函數
時,判斷函數![]() 的單調性;
的單調性;
(2)當![]() 有兩個極值點時,求a的取值范圍,并證明
有兩個極值點時,求a的取值范圍,并證明![]() 的極大值大于2.
的極大值大于2.
【答案】(1)![]() 為(0,+∞)上的減函數.(2)見解析
為(0,+∞)上的減函數.(2)見解析
【解析】
(1)求出函數的導數,法1:結合二次函數的性質判斷導函數的符號,求出函數的單調性即可;法2:令h(x)=(-x2+3x-3)ex-a,根據函數的單調性求出h(x)的最大值,判斷即可;(2)令h(x)=(-x2+3x-3)ex-a,求出函數的導數,根據函數的單調性得到h(x)=0有兩不等實數根x1,x2(x1<x2),求出a的范圍,求出f(x)的極大值判斷即可.
(1)由題知![]() .
.
方法1:由于![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,從而
,從而![]() ,
,
于是![]() 為(0,+∞)上的減函數.
為(0,+∞)上的減函數.
方法2:令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 為增函數;當
為增函數;當![]() 時,
時,![]() ,
,![]() 為減函數.
為減函數.
則![]() .由于
.由于![]() ,所以
,所以![]() ,
,
于是![]() 為(0,+∞)上的減函數.
為(0,+∞)上的減函數.
(2)令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 為增函數;當
為增函數;當![]() 時,
時,![]() ,
, ![]() 為減函數.
為減函數.
當x趨近于![]() 時,
時, ![]() 趨近于
趨近于![]() ,
,
由于![]() 有兩個極值點,所以
有兩個極值點,所以![]() 有兩不等實根,即
有兩不等實根,即![]() 有兩不等實數根
有兩不等實數根![]() (
(![]() ).
).
則有![]() 解得
解得![]() .可知
.可知![]() ,
,
又![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增;當
單調遞增;當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
則函數![]() 在
在![]() 時取極小值,
時取極小值,![]() 在
在![]() 時取極大值.
時取極大值.
即![]() ,
,
而![]() ,即
,即![]() ,
,
所以極大值![]() .當
.當![]() 時,
時,![]() 恒成立,
恒成立,
故![]() 為
為![]() 上的減函數,所以
上的減函數,所以![]()


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,橢圓M:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,左右頂點分別為A,B,線段AB的長為4.P在橢圓M上且位于第一象限,過點A,B分別作l1⊥PA,l2⊥PB,直線l1,l2交于點C.
,左右頂點分別為A,B,線段AB的長為4.P在橢圓M上且位于第一象限,過點A,B分別作l1⊥PA,l2⊥PB,直線l1,l2交于點C.

(1)若點C的橫坐標為﹣1,求P點的坐標;
(2)直線l1與橢圓M的另一交點為Q,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 為
為![]() 的中點,以
的中點,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且二面角
的位置,且二面角![]() 為直二面角,連結
為直二面角,連結![]() .
.
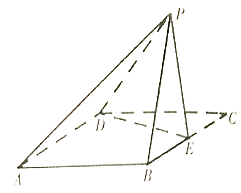
(1)記平面![]() 與平面
與平面![]() 相較于
相較于![]() ,在圖中作出
,在圖中作出![]() ,并說明畫法;
,并說明畫法;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位為了響應疫情期間有序復工復產的號召,組織從疫區回來的甲、乙、丙、丁4名員工進行核酸檢測,現采用抽簽法決定檢測順序,在“員工甲不是第一個檢測,員工乙不是最后一個檢測”的條件下,員工丙第一個檢測的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新高考改革后,國家只統一考試數學和語文,英語學科改為參加等級考試,每年考兩次,分別放在每個學年的上、下學期,物理、化學、生物、地理、歷史、政治這六科則以該省的省會考成績為準.考生從中選擇三科成績,參加大學相關院系的錄取.
(1)若英語等級考試成績有一次為優,即可達到某211院校的錄取要求.假設某個學生參加每次等級考試事件是獨立的,且該生英語等級考試成績為優的概率都是![]() ,求該生在高二上學期的英語等級考試成績才為優的概率;
,求該生在高二上學期的英語等級考試成績才為優的概率;
(2)據預測,要想報考該211院校的相關院系,省會考的成績至少在90分以上,才有可能被該校錄取.假設該生在省會考六科的成績,考到90分以上概率都是![]() ,設該生在省會考時考到90分以上的科目數為
,設該生在省會考時考到90分以上的科目數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接![]() 年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了
年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了![]() 名學生,將他們的比賽成績(滿分為
名學生,將他們的比賽成績(滿分為![]() 分)分為
分)分為![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
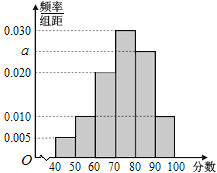
(1)求![]() 的值;
的值;
(2)記![]() 表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于
表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于![]() 分”,估計
分”,估計![]() 的概率;
的概率;
(3)在抽取的![]() 名學生中,規定:比賽成績不低于
名學生中,規定:比賽成績不低于![]() 分為“優秀”,比賽成績低于
分為“優秀”,比賽成績低于![]() 分為“非優秀”.請將下面的
分為“非優秀”.請將下面的![]() 列聯表補充完整,并判斷是否有
列聯表補充完整,并判斷是否有![]() 的把握認為“比賽成績是否優秀與性別有關”?
的把握認為“比賽成績是否優秀與性別有關”?
優秀 | 非優秀 | 合計 | |
男生 |
| ||
女生 |
| ||
合計 |
|
參考公式及數據: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com