
【題目】已知函數(shù)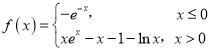 ,則函數(shù)
,則函數(shù)![]() 的零點個數(shù)為( )(
的零點個數(shù)為( )(![]() 是自然對數(shù)的底數(shù))
是自然對數(shù)的底數(shù))
A.6B.5C.4D.3
【答案】B
【解析】
利用導數(shù)研究函數(shù)![]() 的性質,如單調性,函數(shù)值的變化趨勢和,函數(shù)的極值.再研究方程
的性質,如單調性,函數(shù)值的變化趨勢和,函數(shù)的極值.再研究方程![]() 的解的個數(shù),即直線
的解的個數(shù),即直線![]() 與函數(shù)
與函數(shù)![]() 的公共點的的取值,從而利用函數(shù)
的公共點的的取值,從而利用函數(shù)![]() 的性質求得
的性質求得![]() 零點個數(shù).
零點個數(shù).
![]() 時,
時,![]() 是增函數(shù),
是增函數(shù),![]() ,
,
![]() 時,
時,![]() ,
,![]() ,顯然
,顯然![]() ,
,
由![]() ,
,

作出![]() 和
和![]() 的圖象,如圖,
的圖象,如圖,![]() 是增函數(shù),
是增函數(shù),![]() 在
在![]() 是減函數(shù)
是減函數(shù)
它們有一個交點,設交點橫坐標為![]() ,易得
,易得![]() ,
,![]() ,
,
在![]() 時,
時,![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,![]() 是
是![]() 的極小值,也是在
的極小值,也是在![]() 時的最小值.
時的最小值.![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
![]() 時,
時,![]() ,
,![]() 時,
時,![]() .作出
.作出![]() 的大致圖象,作直線
的大致圖象,作直線![]() ,如圖,
,如圖,![]() 時
時![]() 與
與![]() 的圖象有兩個交點,即
的圖象有兩個交點,即![]() 有兩個解
有兩個解![]() ,
,![]() .
.
![]() 時,
時,![]() ,
,![]() ,由
,由![]() 得
得![]() ,而
,而![]() 時,
時,![]() ,
,![]() ,所以直線
,所以直線![]() 與
與![]() 在
在![]() 處相切.即
處相切.即![]() 時方程
時方程![]() 有一個解
有一個解![]() .
.
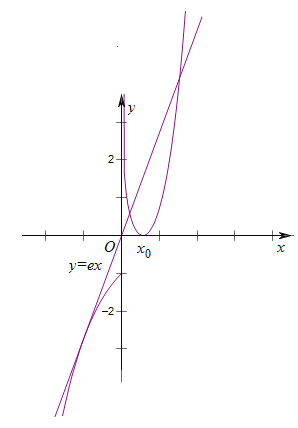
![]() ,令
,令![]() ,則
,則![]() ,由上討論知方程
,由上討論知方程![]() 有三個解:
有三個解:![]() (
(![]() )
)
而![]() 有一個解,
有一個解,![]() 和
和![]() 都有兩個解,所以
都有兩個解,所以![]() 有5個解,
有5個解,
即函數(shù)![]() 有5個零點.
有5個零點.
故選:B.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() ,在以坐標原點為極點,
,在以坐標原點為極點,![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的參數(shù)方程和曲線
的參數(shù)方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,設點
兩點,設點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《孫子算經》是中國古代重要的數(shù)學著作.其中的一道題“今有木,方三尺,高三尺,欲方五寸作枕一枚.問:得幾何?”意思是:“有一塊棱長為3尺的正方體方木,要把它作成邊長為5寸的正方體枕頭,可作多少個?”現(xiàn)有這樣的一個正方體木料,其外周已涂上油漆,則從切割后的正方體枕頭中任取一塊,恰有一面涂上油漆的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,
,![]() 是橢圓上關于原點
是橢圓上關于原點![]() 對稱的兩個動點,當點
對稱的兩個動點,當點![]() 的坐標為
的坐標為![]() 時,
時,![]() 的周長恰為
的周長恰為![]() .
.
(1)求橢圓的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點,且
兩點,且![]()
![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚.太極圖展現(xiàn)了一種相互轉化,相對統(tǒng)一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩個部分的函數(shù)稱為圓
的周長和面積同時等分成兩個部分的函數(shù)稱為圓![]() 的一個“太極函數(shù)”.現(xiàn)有下列說法:①對于圓
的一個“太極函數(shù)”.現(xiàn)有下列說法:①對于圓![]() :
:![]() 的所有非常數(shù)函數(shù)的太極函數(shù)中,一定不能為偶函數(shù);②函數(shù)
的所有非常數(shù)函數(shù)的太極函數(shù)中,一定不能為偶函數(shù);②函數(shù)![]() 是圓
是圓![]() :
:![]() 的一個太極函數(shù);③存在圓
的一個太極函數(shù);③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的一個太極函數(shù);④直線
的一個太極函數(shù);④直線![]() 所對應的函數(shù)一定是圓
所對應的函數(shù)一定是圓![]() :
:![]() (
(![]() )的太極函數(shù);⑤若函數(shù)
)的太極函數(shù);⑤若函數(shù)![]() (
(![]() )是圓
)是圓![]() :
:![]() 的太極函數(shù),則
的太極函數(shù),則![]() .其中正確的是__________.
.其中正確的是__________.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“工資條里顯紅利,個稅新政人民心”.隨著2019年新年鐘聲的敲響,我國自1980年以來,力度最大的一次個人所得稅(簡稱個稅)改革迎來了全面實施的階段.2019年1月1日實施的個稅新政主要內容包括:(1)個稅起征點為5000元;(2)每月應納稅所得額(含稅)=收入-個稅起征點-專項附加扣除;(3)專項附加扣除包括住房、子女教育和贍養(yǎng)老人等.
新舊個稅政策下每月應納稅所得額(含稅)計算方法及其對應的稅率表如下:
舊個稅稅率表(個稅起征點3500元) | 新個稅稅率表(個稅起征點5000元) | |||
繳稅級數(shù) | 每月應納稅所得額(含稅)=收入-個稅起征點 | 稅率(%) | 每月應納稅所得額(含稅)=收入-個稅起征點-專項附加扣除 | 稅率(%) |
1 | 不超過1500元部分 | 3 | 不超過3000元部分 | 3 |
2 | 超過1500元至4500元部分 | 10 | 超過3000元至12000元部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 超過12000元至25000元的部分 | 20 |
4 | 超過9000元至35000元的部分 | 25 | 超過25000元至35000元的部分 | 25 |
5 | 超過35000元至55000元部分 | 30 | 超過35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
隨機抽取某市1000名同一收入層級的![]() 從業(yè)者的相關資料,經統(tǒng)計分析,預估他們2019年的人均月收入24000元.統(tǒng)計資料還表明,他們均符合住房專項扣除;同時,他們每人至多只有一個符合子女教育扣除的孩子,并且他們之中既不符合子女教育扣除又不符合贍養(yǎng)老人扣除、只符合子女教育扣除但不符合贍養(yǎng)老人扣除、只符合贍養(yǎng)老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合贍養(yǎng)老人扣除的人數(shù)之比是2:1:1:1;此外,他們均不符合其他專項附加扣除.新個稅政策下該市的專項附加扣除標準為:住房1000元/月,子女教育每孩1000元/月,贍養(yǎng)老人2000元/月等。
從業(yè)者的相關資料,經統(tǒng)計分析,預估他們2019年的人均月收入24000元.統(tǒng)計資料還表明,他們均符合住房專項扣除;同時,他們每人至多只有一個符合子女教育扣除的孩子,并且他們之中既不符合子女教育扣除又不符合贍養(yǎng)老人扣除、只符合子女教育扣除但不符合贍養(yǎng)老人扣除、只符合贍養(yǎng)老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合贍養(yǎng)老人扣除的人數(shù)之比是2:1:1:1;此外,他們均不符合其他專項附加扣除.新個稅政策下該市的專項附加扣除標準為:住房1000元/月,子女教育每孩1000元/月,贍養(yǎng)老人2000元/月等。
假設該市該收入層級的![]() 從業(yè)者都獨自享受專項附加扣除,將預估的該市該收入層級的
從業(yè)者都獨自享受專項附加扣除,將預估的該市該收入層級的![]() 從業(yè)者的人均月收入視為其個人月收入.根據(jù)樣本估計總體的思想,解決如下問題:
從業(yè)者的人均月收入視為其個人月收入.根據(jù)樣本估計總體的思想,解決如下問題:
(1)設該市該收入層級的![]() 從業(yè)者2019年月繳個稅為
從業(yè)者2019年月繳個稅為![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根據(jù)新舊個稅方案,估計從2019年1月開始,經過多少個月,該市該收入層級的![]() 從業(yè)者各月少繳交的個稅之和就超過2019年的月收入?
從業(yè)者各月少繳交的個稅之和就超過2019年的月收入?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于數(shù)列![]() ,定義“
,定義“![]() 變換”:
變換”:![]() 將數(shù)列
將數(shù)列![]() 變換成數(shù)列
變換成數(shù)列![]() ,其中
,其中![]() ,且
,且![]() ,這種“
,這種“![]() 變換”記作
變換”記作![]() .繼續(xù)對數(shù)列
.繼續(xù)對數(shù)列![]() 進行“
進行“![]() 變換”,得到數(shù)列
變換”,得到數(shù)列![]() ,依此類推,當?shù)玫降臄?shù)列各項均為
,依此類推,當?shù)玫降臄?shù)列各項均為![]() 時變換結束.
時變換結束.
(1)試問![]() 和
和![]() 經過不斷的“
經過不斷的“![]() 變換”能否結束?若能,請依次寫出經過“
變換”能否結束?若能,請依次寫出經過“![]() 變換”得到的各數(shù)列;若不能,說明理由;
變換”得到的各數(shù)列;若不能,說明理由;
(2)求![]() 經過有限次“
經過有限次“![]() 變換”后能夠結束的充要條件;
變換”后能夠結束的充要條件;
(3)證明:![]() 一定能經過有限次“
一定能經過有限次“![]() 變換”后結束.
變換”后結束.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com