
【題目】某學校為了支持生物課程基地研究植物生長,計劃利用學校空地建造一間室內面積為900m2的矩形溫室,在溫室內劃出三塊全等的矩形區域,分別種植三種植物,相鄰矩形區域之間間隔1m,三塊矩形區域的前、后與內墻各保留 1m 寬的通道,左、右兩塊矩形區域分別與相鄰的左右內墻保留 3m 寬的通道,如圖.設矩形溫室的室內長為x(m),三塊種植植物的矩形區域的總面積為S(m2). 
(1)求S關于x的函數關系式;
(2)求S的最大值,及此時長X的值.
【答案】
(1)解:由題意:室內面積為900m2的矩形,長為x(m),則寬為: ![]() ,
,
三塊種植植物的矩形長度為x﹣8,則寬為 ![]() ,
,
植物的矩形區域的總面積為S= ![]() ,(450>x>8)
,(450>x>8)
(2)解:由(1)可得S= ![]() ,(450>x>8)
,(450>x>8)
化簡可得:S=916﹣(2x ![]() ),
),
∵2x ![]() ≥2
≥2 ![]() =240,(當且僅當x=60時取等號)
=240,(當且僅當x=60時取等號)
∴Smax=916﹣240=676(m2)
此時長為x=60.
故得S的最大值676平方米,長度為60米.
【解析】(1)根據題意,室內面積為900m2的矩形,長為x(m),則寬為: ![]() ,三塊種植植物的矩形長度為x﹣8,則寬為
,三塊種植植物的矩形長度為x﹣8,則寬為 ![]() ,植植物的矩形區域的總面積為S=長×寬,可得S關于x的函數關系式.(2)利用基本不等式的性質求解S的最大值以及長度x的值.
,植植物的矩形區域的總面積為S=長×寬,可得S關于x的函數關系式.(2)利用基本不等式的性質求解S的最大值以及長度x的值.


科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱(側棱與底面垂直的棱柱)ABC﹣A1B1C1中,點G是AC的中點.

(1)求證:B1C∥平面 A1BG;
(2)若AB=BC, ![]() ,求證:AC1⊥A1B.
,求證:AC1⊥A1B.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】超市某種綠色食品,過去20個月該食品的月市場需求量![]() (單位:
(單位: ![]() ,
, ![]() )即每月銷售的數據記錄如下:
)即每月銷售的數據記錄如下:
137 108 114 121 115 135 122 140 128 139
125 140 130 125 105 115 133 124 149 115
對這20個數據按組距10進行分組,并統計整理,繪制了如下尚不完整的統計圖表:

(Ⅰ)寫出![]() ,
, ![]() 的值.若視
的值.若視![]() 分布在各區間內的頻率為相應的概率,試計算
分布在各區間內的頻率為相應的概率,試計算![]() ;
;
(Ⅱ)記![]() 組月市場需求量數據的平均數與方差分別為
組月市場需求量數據的平均數與方差分別為![]() ,
, ![]() ,
, ![]() 組月市場需求量數據的平均數與方差分別為
組月市場需求量數據的平均數與方差分別為![]() ,
, ![]() ,試分別比較
,試分別比較![]() 與
與![]() ,
, ![]() 與
與![]() 的大小;(只需寫出結論)
的大小;(只需寫出結論)
(Ⅲ)為保證該綠色產品的質量,超市規定該產品僅在每月一日上架銷售,每月最后一日對所有未售出的產品進行下架處理.若超市每售出![]() 該綠色食品可獲利潤5元,未售出的食品每
該綠色食品可獲利潤5元,未售出的食品每![]() 虧損3元,并且超市為下一個月采購了
虧損3元,并且超市為下一個月采購了![]() 該綠色食品,求超市下一個月銷售該綠色食品的利潤
該綠色食品,求超市下一個月銷售該綠色食品的利潤![]() 的分布列及數學期望
的分布列及數學期望![]() .(以分組的區間中點值代表該組的各個值,并以月市場需求量落入該區間的頻率作為月市場需求量取該組區間中點值的概率)
.(以分組的區間中點值代表該組的各個值,并以月市場需求量落入該區間的頻率作為月市場需求量取該組區間中點值的概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}滿足:a1=1,a2+a6=14;正項等比數列{bn}滿足:b1=2,b3=8.
(Ⅰ) 求數列{an},{bn}的通項公式an , bn;
(Ⅱ)求數列{anbn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點, ![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() .
.
(1)寫出曲線![]() ,
, ![]() 的普通方程;
的普通方程;
(2)過曲線![]() 的右焦點
的右焦點![]() 作傾斜角為
作傾斜角為![]() 的直線
的直線![]() ,該直線與曲線
,該直線與曲線![]() 相交于不同的兩點
相交于不同的兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分別是PC,PD,BC的中點. 
(1)求證:平面PAB∥平面EFG;
(2)在線段PB上確定一點Q,使PC⊥平面ADQ,并給出證明;
(3)求出D到平面EFG的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一個關于平面圖形的命題:如圖,同一個平面內有兩個邊長都是a的正方形,其中一個的某頂點在另一個的中心,則這兩個正方形重疊部分的面積恒為 ![]() .類比到空間,有兩個棱長均為a的正方體,其中一個的某頂點在另一個的中心,則這兩個正方體重疊部分的體積恒為 .
.類比到空間,有兩個棱長均為a的正方體,其中一個的某頂點在另一個的中心,則這兩個正方體重疊部分的體積恒為 . 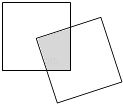
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com