
【題目】如圖,四棱錐![]() 的底面是正方形,
的底面是正方形, ![]() 底面
底面![]() ,
, ![]() ,點
,點![]() 分別在棱
分別在棱![]() 上,且
上,且![]() 平面
平面![]() .
.
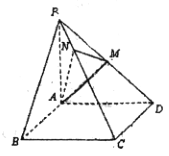
(1)求證: ![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(3)求二面角![]() 的余弦值
的余弦值
【答案】(1)見解析(2)![]() (3)
(3)![]()
【解析】試題分析:(1)先根據線面垂直性質定理得![]() ,再由
,再由![]() ,以及線面垂直判定定理得
,以及線面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() ,由
,由![]() 平面
平面![]() ,有
,有![]() ,再由線面垂直判定定理得
,再由線面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() ;(2)因為
;(2)因為![]() 平面
平面![]() ,所以
,所以![]() 為
為![]() 在平面
在平面![]() 內的射影,延長
內的射影,延長![]() 交于點
交于點![]() ,則
,則![]() 為
為![]() (即
(即![]() )與平面
)與平面![]() 所成的角,解直角三角形得線面角正弦值.(3)以空間向量求角二面角,先建立空間直角坐標系,設立各點坐標,列方程組解平面法向量,由向量數量積得兩法向量夾角余弦值,最后根據二面角與兩法向量關系得結果
所成的角,解直角三角形得線面角正弦值.(3)以空間向量求角二面角,先建立空間直角坐標系,設立各點坐標,列方程組解平面法向量,由向量數量積得兩法向量夾角余弦值,最后根據二面角與兩法向量關系得結果
試題解析:(1)因為四邊形![]() 是正方形,所以
是正方形,所以![]() ,
,
又因為![]() 底面
底面![]() ,所以
,所以![]() ,故
,故![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,則
,則![]() ,
,
而![]() 平面
平面![]() ,有
,有![]() ,則
,則![]() 平面
平面![]() ,
,
故![]() .
.
(2)如圖,延長![]() 交于點
交于點![]() ,因為
,因為![]() 平面
平面![]() ,
,
所以![]() 為
為![]() 在平面
在平面![]() 內的射影,故
內的射影,故![]() 為
為![]() (即
(即![]() )與平面
)與平面![]() 所成的角,
所成的角,
又因為![]() ,
, ![]() ,則有
,則有![]() ,
,
在![]() 中,
中, ![]() ,
,
故![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
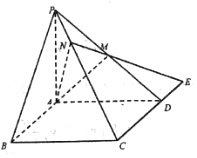
(3)分別以![]() 為
為![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系, ![]() ,
, ![]()
所以![]() ,
, ![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,
,
那么![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,由(1)知,平面
,由(1)知,平面![]() 的法向量
的法向量![]() ,
,
設所求二面角![]() 的大小為
的大小為![]() ,且為銳角,所以
,且為銳角,所以![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某企業開發一種新產品,現準備投入適當的廣告費,對產品進行促銷,在一年內,預計年銷量Q(萬件)與廣告費x(萬件)之間的函數關系為 ![]() ,已知生產此產品的年固定投入為3萬元,每年產1萬件此產品仍需要投入32萬元,若年銷售額為(32Q+3)150%+x50%,而當年產銷量相等.
,已知生產此產品的年固定投入為3萬元,每年產1萬件此產品仍需要投入32萬元,若年銷售額為(32Q+3)150%+x50%,而當年產銷量相等.
(1)試將年利潤P(萬件)表示為年廣告費x(萬元)的函數;
(2)當年廣告費投入多少萬元時,企業年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x ![]() (m∈Z)為偶函數,且在(0,+∞)上為增函數.
(m∈Z)為偶函數,且在(0,+∞)上為增函數.
(1)求m的值,并確定f(x)的解析式;
(2)若函數g(x)=loga(f(x)﹣ax+2)在區間(1,+∞)上恒為正值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log3 ![]() ,g(x)=﹣2ax+a+1,h(x)=f(x)+g(x).
,g(x)=﹣2ax+a+1,h(x)=f(x)+g(x).
(Ⅰ)當a=﹣1時,證明h(x)是奇函數;
(Ⅱ)若關于x的方程f(x)=log3g(x)有兩個不等實數根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了支持生物課程基地研究植物生長,計劃利用學校空地建造一間室內面積為900m2的矩形溫室,在溫室內劃出三塊全等的矩形區域,分別種植三種植物,相鄰矩形區域之間間隔1m,三塊矩形區域的前、后與內墻各保留 1m 寬的通道,左、右兩塊矩形區域分別與相鄰的左右內墻保留 3m 寬的通道,如圖.設矩形溫室的室內長為x(m),三塊種植植物的矩形區域的總面積為S(m2). 
(1)求S關于x的函數關系式;
(2)求S的最大值,及此時長X的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線C1:y2=2px與橢圓C2: ![]() 在第一象限的交點為B,O為坐標原點,A為橢圓的右頂點,△OAB的面積為
在第一象限的交點為B,O為坐標原點,A為橢圓的右頂點,△OAB的面積為 ![]() .
. 
(1)求拋物線C1的方程;
(2)過A點作直線L交C1于C、D兩點,求線段CD長度的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com