Question

【題目】已知橢圓的左、右焦點分別為，右頂點為，且離心率為.

（1）求橢圓的標準方程；

（2）互相平行的兩條直線分別過，且直線與橢圓交于兩點，直線與橢圓交于，兩點，若四邊形的面積為，求直線的方程.

Answer 1

【答案】（1）（2）直線的方程為或；相應地，直線的方程或

【解析】

由題意知,結合離心率和之間的關系即可求解;

由知,, 由對稱性知四邊形為平行四邊形,分斜率存在和不存在兩種情況分別求出四邊形的面積的表達式,進而求出直線方程.

由題意知，因為橢圓的離心率為，

所以，解得，所以，

所以橢圓的標準方程為.

（2）由（1）知焦點的坐標為，

①當直線的斜率不存在時，其直線方程分別是，

將代入橢圓，得，解得，

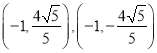所以的坐標分別為或；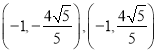

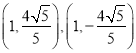同理可得,的坐標分別為或；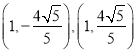

則四邊形的面積不合題意，

②當直線的斜率存在時，設此時直線的方程分別為.

聯立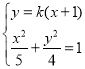消去，得，

設點，，則，，

所以

.

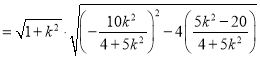
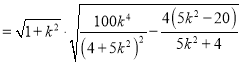
而直線之間的距離為，

由對稱性知四邊形為平行四邊形，

所以四邊形的面積為

，

又四邊形的面積為，所以，

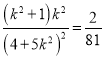得，平方，化簡得，

解得（舍去）或，所以，

故直線的方程為或；相應地，直線的方程或.