
【題目】讀書可以使人保持思想活力,讓人得到智慧啟發,讓人滋養浩然正氣書籍是文化的重要載體,讀書是承繼文化的重要方式某地區為了解學生課余時間的讀書情況,隨機抽取了![]() 名學生進行調查,根據調查得到的學生日均課余讀書時間繪制成如圖所示的頻率分布直方圖,將日均課余讀書時間不低于
名學生進行調查,根據調查得到的學生日均課余讀書時間繪制成如圖所示的頻率分布直方圖,將日均課余讀書時間不低于![]() 分鐘的學生稱為“讀書之星”,日均課余讀書時間低于
分鐘的學生稱為“讀書之星”,日均課余讀書時間低于![]() 分鐘的學生稱為“非讀書之星”:已知抽取的樣本中日均課余讀書時間低于
分鐘的學生稱為“非讀書之星”:已知抽取的樣本中日均課余讀書時間低于![]() 分鐘的有
分鐘的有![]() 人
人
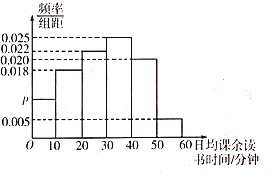
(1)求![]() 的值;
的值;
(2)根據已知條件完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 以上的把握認為“讀書之星”與性別有關?
以上的把握認為“讀書之星”與性別有關?
非讀書之星 | 讀書之星 | 總計 | |
男 | |||
女 |
|
| |
總計 |
(3)將上述調查所得到的頻率視為概率,現從該地區大量學生中,隨機抽取![]() 名學生,每次抽取
名學生,每次抽取![]() 名,已知每個人是否被抽到互不影響,記被抽取的“讀書之星”人數為隨機變量
名,已知每個人是否被抽到互不影響,記被抽取的“讀書之星”人數為隨機變量![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]()
附: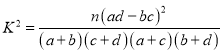 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)![]() ,n=100,(2)表見解析,沒有
,n=100,(2)表見解析,沒有![]() 以上的把握認為“讀書之星”與性別有關(3)分布列見解析,
以上的把握認為“讀書之星”與性別有關(3)分布列見解析,![]()
【解析】
(1)首先根據頻率和為1求![]() ,再根據頻率,頻數和樣本容量的關系求
,再根據頻率,頻數和樣本容量的關系求![]() ;
;
(2)首先計算“讀書之星”的人數,然后再依次填寫![]() 列聯表;并根據公式計算
列聯表;并根據公式計算![]() 和
和![]() 比較大小,做出判斷;
比較大小,做出判斷;
(3)從該地區學生中抽取一名學生是“讀書之星”的概率為![]() ,由題意可知
,由題意可知![]()
并求分布列和數學期望.
(1)![]()
解得:![]() ,
,
所以![]() .
.
(2)因為![]() ,所以“讀書之星”有
,所以“讀書之星”有![]()
從而![]() 列聯表如下圖所示:
列聯表如下圖所示:
非讀書之星 | 讀書之星 | 總計 | |
男 |
|
|
|
女 |
|
|
|
總計 |
|
|
|
將![]() 列聯表中的數據代入公式計算得
列聯表中的數據代入公式計算得
![]()
因為![]() ,所以沒有
,所以沒有![]() 以上的把握認為“讀書之星”與性別有關
以上的把握認為“讀書之星”與性別有關
(3)將頻率視為概率,即從該地區學生中抽取一名學生是“讀書之星”的概率為![]() .
.
由題意可知![]()
所以![]()
![]() ,
,
![]()
![]()
所以![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
故![]() .
.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在正常數
,若存在正常數![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 成立,我們稱函數
成立,我們稱函數![]() 為“
為“![]() 同比不減函數”.
同比不減函數”.
(1)求證:對任意正常數![]() ,
,![]() 都不是“
都不是“![]() 同比不減函數”;
同比不減函數”;
(2)若函數![]() 是“
是“![]() 同比不減函數”,求
同比不減函數”,求![]() 的取值范圍;
的取值范圍;
(3)是否存在正常數![]() ,使得函數
,使得函數![]() 為“
為“![]() 同比不減函數”,若存在,求
同比不減函數”,若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且2acosB=2c﹣b.
(1)求∠A的大小;
(2)若△ABC的外接圓的半徑為![]() ,面積為
,面積為![]() ,求△ABC的周長.
,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了鼓勵職員工作熱情,某公司對每位職員一年來的工作業績按月進行考評打分;年終按照職員的月平均值評選公司最佳職員并給予相應獎勵.已知職員![]() 一年來的工作業績分數的莖葉圖如圖所示:
一年來的工作業績分數的莖葉圖如圖所示:
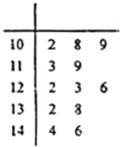
(1)根據職員![]() 的業績莖葉圖求出他這一年的工作業績的中位數和平均數;
的業績莖葉圖求出他這一年的工作業績的中位數和平均數;
(2)由于職員![]() 的業績高,被公司評為年度最佳職員,在公司年會上通過抽獎形式領取獎金.公司準備了六張卡片,其中一張卡片上標注獎金為6千元,兩張卡片的獎金為4千元,另外三張的獎金為2千元.規則是:獲獎職員
的業績高,被公司評為年度最佳職員,在公司年會上通過抽獎形式領取獎金.公司準備了六張卡片,其中一張卡片上標注獎金為6千元,兩張卡片的獎金為4千元,另外三張的獎金為2千元.規則是:獲獎職員![]() 需要從六張卡片中隨機抽出兩張,這兩張卡片上的金額數之和作為獎金數.求職員
需要從六張卡片中隨機抽出兩張,這兩張卡片上的金額數之和作為獎金數.求職員![]() 獲得獎金6千元的概率;并說明獲得獎金6千元和8千元哪個可能性較大?
獲得獎金6千元的概率;并說明獲得獎金6千元和8千元哪個可能性較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{bn}的前n項和為Tn,且T4=4,b5=6.
(1)求數列{bn}的通項公式;
(2)若正整數n1,n2,…,nt,…滿足5<n1<n2<…<nt,…且b3,b5,![]() ,
,![]() ,…,
,…,![]() ,…成等比數列,求數列{nt}的通項公式(t是正整數);
,…成等比數列,求數列{nt}的通項公式(t是正整數);
(3)給出命題:在公比不等于1的等比數列{an}中,前n項和為Sn,若am,am+2,am+1成等差數列,則Sm,Sm+2,Sm+1也成等差數列.試判斷此命題的真假,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著金融市場的發展,越來越多人選擇投資“黃金”作為理財的手段,下面將A市把黃金作為理財產品的投資人的年齡情況統計如下圖所示.
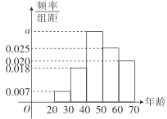
(1)求把黃金作為理財產品的投資者的年齡的中位數;(結果用小數表示,小數點后保留兩位有效數字)
(2)現按照分層抽樣的方法從年齡在![]() 和
和![]() 的投資者中隨機抽取5人,再從這5人中隨機抽取3人進行投資調查,求恰有1人年齡在
的投資者中隨機抽取5人,再從這5人中隨機抽取3人進行投資調查,求恰有1人年齡在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,墻上有一壁畫,最高點![]() 離地面4米,最低點
離地面4米,最低點![]() 離地面2米,觀察者從距離墻
離地面2米,觀察者從距離墻![]() 米,離地面高
米,離地面高![]() 米的
米的![]() 處觀賞該壁畫,設觀賞視角
處觀賞該壁畫,設觀賞視角![]()
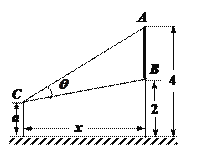
(1)若![]() 問:觀察者離墻多遠時,視角
問:觀察者離墻多遠時,視角![]() 最大?
最大?
(2)若![]() 當
當![]() 變化時,求
變化時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com