
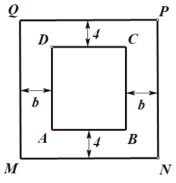
【題目】一酒企為擴大生產(chǎn)規(guī)模,決定新建一個底面為長方形![]() 的室內(nèi)發(fā)酵館,發(fā)酵館內(nèi)有一個無蓋長方體發(fā)酵池,其底面為長方形
的室內(nèi)發(fā)酵館,發(fā)酵館內(nèi)有一個無蓋長方體發(fā)酵池,其底面為長方形![]() (如圖所示),其中
(如圖所示),其中![]() .結(jié)合現(xiàn)有的生產(chǎn)規(guī)模,設(shè)定修建的發(fā)酵池容積為450米
.結(jié)合現(xiàn)有的生產(chǎn)規(guī)模,設(shè)定修建的發(fā)酵池容積為450米![]() ,深2米.若池底和池壁每平方米的造價分別為200元和150元,發(fā)酵池造價總費用不超過65400元
,深2米.若池底和池壁每平方米的造價分別為200元和150元,發(fā)酵池造價總費用不超過65400元
(1)求發(fā)酵池![]() 邊長的范圍;
邊長的范圍;
(2)在建發(fā)酵館時,發(fā)酵池的四周要分別留出兩條寬為4米和![]() 米的走道(
米的走道(![]() 為常數(shù)).問:發(fā)酵池的邊長如何設(shè)計,可使得發(fā)酵館占地面積最小.
為常數(shù)).問:發(fā)酵池的邊長如何設(shè)計,可使得發(fā)酵館占地面積最小.
【答案】(1)![]() (2)當(dāng)
(2)當(dāng)![]() 時,
時,![]() ,
,![]() 米時,發(fā)酵館的占地面積最小;當(dāng)
米時,發(fā)酵館的占地面積最小;當(dāng)![]() 時,
時,![]() 時,發(fā)酵館的占地面積最小;當(dāng)
時,發(fā)酵館的占地面積最小;當(dāng)![]() 時,
時,![]() 米時,發(fā)酵館的占地面積最小.
米時,發(fā)酵館的占地面積最小.
【解析】
(1)設(shè)![]() 米,總費用為
米,總費用為![]() ,解
,解![]() 即可得解;
即可得解;
(2)結(jié)合(1)可得占地面積![]() 結(jié)合導(dǎo)函數(shù)分類討論即可求得最值.
結(jié)合導(dǎo)函數(shù)分類討論即可求得最值.
(1)由題意知:矩形![]() 面積
面積![]() 米
米![]() ,
,
設(shè)![]() 米,則
米,則![]() 米,由題意知:
米,由題意知:![]() ,得
,得![]() ,
,
設(shè)總費用為![]() ,
,
則![]() ,
,
解得:![]() ,又
,又![]() ,故
,故![]() ,
,
所以發(fā)酵池![]() 邊長的范圍是不小于15米,且不超過25米;
邊長的范圍是不小于15米,且不超過25米;
(2)設(shè)發(fā)酵館的占地面積為![]() 由(1)知:
由(1)知:![]() ,
, ![]()
①![]() 時,
時,![]() ,
,![]() 在
在![]() 上遞增,則
上遞增,則![]() ,即
,即![]() 米時,發(fā)酵館的占地面積最小;
米時,發(fā)酵館的占地面積最小;
②![]() 時,
時,![]() ,
,![]() 在
在![]() 上遞減,則
上遞減,則![]() ,即
,即![]() 米時,發(fā)酵館的占地面積最小;
米時,發(fā)酵館的占地面積最小;
③![]() 時,
時,![]() 時,
時,![]() ,
,![]() 遞減;
遞減;![]() 時,
時,![]() 遞增,
遞增,
因此![]() ,即
,即![]() 時,發(fā)酵館的占地面積最小;
時,發(fā)酵館的占地面積最小;
綜上所述:當(dāng)![]() 時,
時,![]() ,
,![]() 米時,發(fā)酵館的占地面積最小;當(dāng)
米時,發(fā)酵館的占地面積最小;當(dāng)![]() 時,
時,![]() 時,發(fā)酵館的占地面積最小;當(dāng)
時,發(fā)酵館的占地面積最小;當(dāng)![]() 時,
時,![]() 米時,發(fā)酵館的占地面積最小.
米時,發(fā)酵館的占地面積最小.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點![]() 、
、![]() 、
、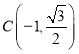 、
、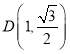 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求橢圓的方程;
(2)已知點![]() 是橢圓的右頂點,作一條平行于
是橢圓的右頂點,作一條平行于![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點,記直線
兩點,記直線![]() 和直線
和直線![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,試判斷
,試判斷![]() 是否為定值?若是,求出該定值;若不是,請說明理由.
是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】曲線![]() 的參數(shù)方程為
的參數(shù)方程為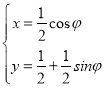 (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標(biāo)系中,曲線
軸的正半軸為極軸的極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與曲線
與曲線![]() ,
,![]() 的交點分別為
的交點分別為![]() 、
、![]() (
(![]() 、
、![]() 異于原點),當(dāng)斜率
異于原點),當(dāng)斜率![]() 時,求
時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為慶祝新中國成立七十周年,巴蜀中學(xué)將舉行“歌唱祖國,喜迎國慶”歌詠比賽活動,《歌唱祖國》,《精忠報國》,《我和我的祖國》等一系列歌曲深受同學(xué)們的青睞,高二某班級就該班是否選擇《精忠報國》作為本班參賽曲目進行投票表決,投票情況如下表.
小組 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
贊成人數(shù) | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
總?cè)藬?shù) | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若從第1小組和第8小組的同學(xué)中各隨機選取2人進行調(diào)查,求所選取的4人中至少有2人贊成《精忠報國》作為本班參賽曲目的概率;
(2)若從第5小組和第7小組的同學(xué)中各隨機選取2人進行調(diào)查,記選取的4人中不贊成《精忠報國》作為本班參賽曲目的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一點,且
上一點,且![]() ,點
,點![]() 是
是![]() 的中點,將
的中點,將![]() 沿著
沿著![]() 折起,使點
折起,使點![]() 運動到點
運動到點![]() 處,且滿足
處,且滿足![]() .
.
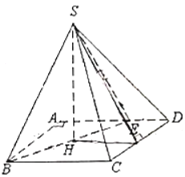
(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,N為CD的中點,M是AC上一點.
中,N為CD的中點,M是AC上一點.
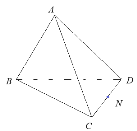
(1)若M為AC的中點,求證:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直線AC與平面BMN所成的角的余弦值。
,求直線AC與平面BMN所成的角的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且與
且與![]() 軸不重合,
軸不重合, ![]() 交圓
交圓![]() 于
于![]() 兩點,過
兩點,過![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
(1)證明![]() 為定值,并寫出點
為定值,并寫出點![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)![]() ,過點
,過點![]() 作直線
作直線![]() ,交點
,交點![]() 的軌跡于
的軌跡于![]() 兩點 (異于
兩點 (異于![]() ),直線
),直線![]() 的斜率分別為
的斜率分別為![]() ,證明:
,證明: ![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com