
 某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據:
某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
分析 (1)把所給的四對數據寫成對應的點的坐標,在坐標系中描出來,得到散點圖.
(2)作出利用最小二乘法來求線性回歸方程的系數的量,求出橫標和縱標的平均數,求出系數,再求出a的值,注意運算不要出錯.
(3)由回歸直線方程預測,記憶力為9的同學的判斷力約為4.
解答 解:(1)把所給的四對數據寫成對應的點的坐標,在坐標系中描出來,得到散點圖.如圖所示:
(2)$\sum_{i=1}^{n}$xiyi=6×2+8×3+10×5+12×6=158,
$\overline{x}$=$\frac{6+8+10+12}{4}$=9,$\overline{y}$=$\frac{2+3+5+6}{4}$=4,
$\sum_{i=1}^{n}$${x}_{1}^{2}$=62+82+102+122=344,
$\stackrel{∧}{b}$=$\frac{158-4×9×4}{344-4×92}$=$\frac{14}{20}$=0.7,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=4-0.7×9=-2.3,
故線性回歸方程為$\stackrel{∧}{y}$=0.7x-2.3.
(3)由回歸直線方程,當x=9時,$\stackrel{∧}{y}$=0.7×9-2.3=6.3-2.3=4,所以預測記憶力為9的同學的判斷力約為4.
點評 本題考查線性回歸方程的求法和應用,本題解題的關鍵是利用最小二乘法做出線性回歸方程的系數,本題是一個近幾年可能出現在高考卷中的題目.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:解答題
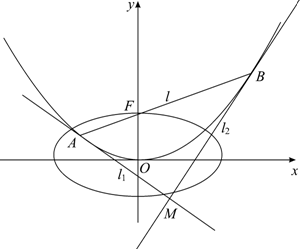 已知拋物線C:x2=4y的焦點為F,過點F作直線l交拋物線C于A、B兩點;橢圓E的中心在原點,焦點在x軸上,點F是它的一個頂點,且其離心率e=$\frac{{\sqrt{3}}}{2}$.
已知拋物線C:x2=4y的焦點為F,過點F作直線l交拋物線C于A、B兩點;橢圓E的中心在原點,焦點在x軸上,點F是它的一個頂點,且其離心率e=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
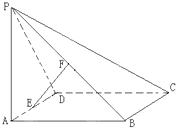 如圖:四棱錐P-ABCD的底面是平行四邊形,∠DAB=60°,平面PAB⊥ABD,
如圖:四棱錐P-ABCD的底面是平行四邊形,∠DAB=60°,平面PAB⊥ABD,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,0) | B. | (0,-1) | C. | (-$\frac{1}{16}$,0) | D. | (0,-$\frac{1}{16}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com