
 =1(α為銳角)和圓(x-m)2+y2=r2相切于點A(4
=1(α為銳角)和圓(x-m)2+y2=r2相切于點A(4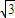 ,4),求α,m,r的值.
,4),求α,m,r的值. ,4)代入雙曲線
,4)代入雙曲線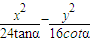 =1(α為銳角),求出α的值,聯立雙曲線和圓的方程,消去y得到關于x的一元二次方程,△=0,和把點A(4
=1(α為銳角),求出α的值,聯立雙曲線和圓的方程,消去y得到關于x的一元二次方程,△=0,和把點A(4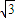 ,4)代入圓(x-m)2+y2=r2,解方程組即可求得m,r的值.
,4)代入圓(x-m)2+y2=r2,解方程組即可求得m,r的值.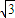 ,4)在雙曲線上,
,4)在雙曲線上,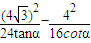 =1,
=1, -tanα=1
-tanα=1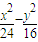 =1(1)
=1(1)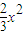 -16,
-16,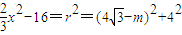 ,
, m-240=0.
m-240=0.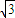 m+400=0,
m+400=0,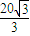 .
.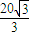 ,0),
,0),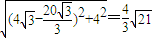 .
.

 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com