
【題目】如圖,四邊形ABCD是梯形,四邊形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE= ![]() CD=2,M是線段AE上的動點.
CD=2,M是線段AE上的動點. 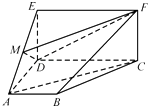
(Ⅰ)試確定點M的位置,使AC∥平面MDF,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求平面MDF將幾何體ADE﹣BCF分成的兩部分的體積之比.
【答案】解:(Ⅰ)當M是線段AE的中點時,AC∥平面MDF.證明如下:
連結CE,交DF于N,連結MN,
由于M、N分別是AE、CE的中點,所以MN∥AC,
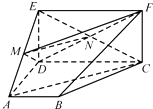
由于MN平面MDF,又AC平面MDF,
所以AC∥平面MDF.
(Ⅱ)如圖,將幾何體ADE﹣BCF補成三棱柱ADE﹣B′CF,
三棱柱ADE﹣B′CF的體積為 ![]() ,
,
則幾何體ADE﹣BCF的體積

VADE﹣BCF=V三棱柱ADE﹣BCF﹣VF﹣BB'C= ![]() .
.
三棱錐F﹣DEM的體積V三棱錐M﹣DEF= ![]() ,
,
故兩部分的體積之比為 ![]() (答1:4,4,4:1均可)
(答1:4,4,4:1均可)
【解析】(Ⅰ)首先,根據所給圖形,得到當M是線段AE的中點時,AC∥平面MDF.然后,根據線面平行的判定定理進行證明即可;(Ⅱ)利用補圖法,將幾何體ADE﹣BCF補成三棱柱ADE﹣B′CF,然后,借助于柱體和椎體的體積公式進行求解即可.
【考點精析】根據題目的已知條件,利用直線與平面平行的判定和直線與平面垂直的判定的相關知識可以得到問題的答案,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 是奇函數,
是奇函數, ![]() 是偶函數.
是偶函數.
(1)求![]() 和
和![]() 的值;
的值;
(2)說明函數![]() 的單調性;若對任意的
的單調性;若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若存在
,若存在![]() ,使不等式
,使不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,如圖描述了甲、乙、丙三輛汽車在不同速度下燃油效率情況,下列敘述中正確的是( ) 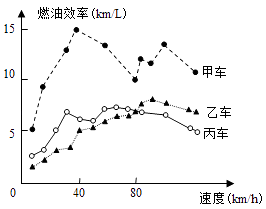
A.消耗1升汽油,乙車最多可行駛5千米
B.以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C.甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D.某城市機動車最高限速80千米/小時,相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若拋物線y2=2px(p>0)上一點到焦點和拋物線對稱軸的距離分別為10和6,則拋物線方程為( )
A.y2=4x
B.y2=36x
C.y2=4x或y2=36x
D.y2=8x或y2=32x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數的定義域;
(2)判斷函數的奇偶性,并證明你的結論;
(3)在函數![]() 圖像上是否存在兩個不同的點
圖像上是否存在兩個不同的點![]() ,使直線
,使直線![]() 垂直
垂直![]() 軸,若存在,求出
軸,若存在,求出![]() 兩點坐標;若不存在,說明理由.
兩點坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】執行如圖所示的程序框圖,則下列說法正確的( ) 
A.a∈(2,4),輸出的i的值為5
B.a∈(4,5),輸出的i的值為5
C.a∈(3,4),輸出的i的值為5
D.a∈(2,4),輸出的i的值為5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程為:
的方程為: ![]() 。
。
(1)求圓![]() 的圓心所在直線方程一般式;
的圓心所在直線方程一般式;
(2)若直線![]() 被圓
被圓![]() 截得弦長為
截得弦長為![]() ,試求實數
,試求實數![]() 的值;
的值;
(3)已知定點![]() ,且點
,且點![]() 是圓
是圓![]() 上兩動點,當
上兩動點,當![]() 可取得最大值為
可取得最大值為![]() 時,求滿足條件的實數
時,求滿足條件的實數![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①如果不同直線![]() 都平行于平面
都平行于平面![]() ,則
,則![]() 一定不相交;
一定不相交;
②如果不同直線![]() 都垂直于平面
都垂直于平面![]() ,則
,則![]() 一定平行;
一定平行;
③如果平面![]() 互相平行,若直線
互相平行,若直線![]() ,直線
,直線![]() ,則
,則![]() ;
;
④如果平面![]() 互相垂直,且直線
互相垂直,且直線![]() 也互相垂直,若
也互相垂直,若![]() ,則
,則![]() ;
;
其中正確的個數為( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過點(0,2)的直線l與中心在原點,焦點在x軸上且離心率為 ![]() 的橢圓C相交于A、B兩點,直線
的橢圓C相交于A、B兩點,直線 ![]() 過線段AB的中點,同時橢圓C上存在一點與右焦點關于直線l對稱.
過線段AB的中點,同時橢圓C上存在一點與右焦點關于直線l對稱.
(1)求直線l的方程;
(2)求橢圓C的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com