
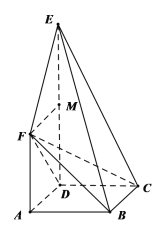
【題目】如圖,在多面體![]() 中,正方形
中,正方形![]() 與梯形
與梯形![]() 所在平面互相垂直,已知
所在平面互相垂直,已知![]() ,
,![]() ,
,![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)由正方形的性質(zhì)及平面![]()
![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,即
,即![]() ,取
,取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,可證得
,可證得![]() ,即可求證;
,即可求證;
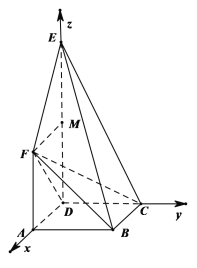
(2)以![]() 為原點(diǎn),以
為原點(diǎn),以![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系![]() ,由(1)可得
,由(1)可得![]() 為平面
為平面![]() 的一個法向量,再求得平面
的一個法向量,再求得平面![]() 的一個法向量
的一個法向量![]() ,進(jìn)而利用余弦定理求解即可.
,進(jìn)而利用余弦定理求解即可.
(1)證明:![]() 正方形
正方形![]() ,
,![]() ,
,
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,易得四邊形
,易得四邊形![]() 為正方形,
為正方形,![]() ,
,
則![]() ,即
,即![]() ,
,
又![]() ,則
,則![]() 平面
平面![]() .
.
(2)![]() 且
且![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,易知
,易知![]() 兩兩垂直,
兩兩垂直,
以![]() 為原點(diǎn),以
為原點(diǎn),以![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系![]() ,如圖所示,
,如圖所示,
易得![]() ,則
,則![]() ,
,![]() ,
,
由(1)得![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
令![]()
![]() 為平面
為平面![]() 的一個法向量,則
的一個法向量,則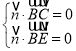 ,得
,得![]() ,
,
不妨令![]() ,則
,則![]() ,故
,故![]()
![]() ,
,
令所求二面角為![]() ,則
,則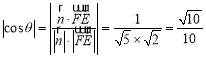 ,
,
則![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),將曲線
為參數(shù)),將曲線![]() 上各點(diǎn)縱坐標(biāo)伸長到原來的
上各點(diǎn)縱坐標(biāo)伸長到原來的![]() 倍(橫坐標(biāo)不變),得到曲線
倍(橫坐標(biāo)不變),得到曲線![]() .以坐標(biāo)原點(diǎn)
.以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,直線
軸的正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出曲線![]() 的極坐標(biāo)方程與直線
的極坐標(biāo)方程與直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)曲線![]() 上是否存在不同的兩點(diǎn)
上是否存在不同的兩點(diǎn)![]() ,
,![]() (以上兩點(diǎn)坐標(biāo)均為極坐標(biāo),
(以上兩點(diǎn)坐標(biāo)均為極坐標(biāo),![]() ,
,![]() ,
,![]() ,
,![]() ),使點(diǎn)
),使點(diǎn)![]() 、
、![]() 到
到![]() 的距離都為
的距離都為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為助力湖北新冠疫情后的經(jīng)濟(jì)復(fù)蘇,某電商平臺為某工廠的產(chǎn)品開設(shè)直播帶貨專場.為了對該產(chǎn)品進(jìn)行合理定價,用不同的單價在平臺試銷,得到如下數(shù)據(jù):
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根據(jù)以上數(shù)據(jù),求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該產(chǎn)品成本是4元/件,假設(shè)該產(chǎn)品全部賣出,預(yù)測把單價定為多少時,工廠獲得最大利潤?
(參考公式:回歸方程![]() ,其中
,其中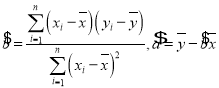 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《周髀算經(jīng)》是中國古代重要的數(shù)學(xué)著作,其記載的“日月歷法”曰:“陰陽之?dāng)?shù),日月之法,十九歲為一章,四章為一部,部七十六歲,二十部為一遂,遂千百五二十歲,….生數(shù)皆終,萬物復(fù)蘇,天以更元作紀(jì)歷”,某老年公寓住有20位老人,他們的年齡(都為正整數(shù))之和恰好為一遂,其中年長者已是奔百之齡(年齡介于90至100),其余19人的年齡依次相差一歲,則年長者的年齡為( )
A.94B.95C.96D.98
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2016年某高校藝術(shù)類考試中,共有6位選手參加,其中3位女生,3位男生,現(xiàn)這6名考生依次出場進(jìn)行才藝展出,如果3位男生中任何2人都不能連續(xù)出場,且女生甲不能排第一個,那么這6名考生出場順序的排法種數(shù)為( )
A.108B.120C.132D.144
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某科研團(tuán)隊(duì)對![]() 例新冠肺炎確診患者的臨床特征進(jìn)行了回顧性分析.其中
例新冠肺炎確診患者的臨床特征進(jìn)行了回顧性分析.其中![]() 名吸煙患者中,重癥人數(shù)為
名吸煙患者中,重癥人數(shù)為![]() 人,重癥比例約為
人,重癥比例約為![]() ;
;![]() 名非吸煙患者中,重癥人數(shù)為
名非吸煙患者中,重癥人數(shù)為![]() 人,重癥比例為
人,重癥比例為![]() .
.
(1)根據(jù)以上數(shù)據(jù)完成![]() 列聯(lián)表;
列聯(lián)表;
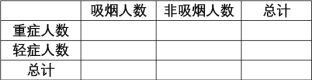
(2)根據(jù)(1)中列聯(lián)表數(shù)據(jù),能否在犯錯誤的概率不超過![]() 的前提下認(rèn)為新冠肺炎重癥與吸煙有關(guān)?
的前提下認(rèn)為新冠肺炎重癥與吸煙有關(guān)?
(3)已知每例重癥患者平均治療費(fèi)用約為![]() 萬元,每例輕癥患者平均治療費(fèi)用約為
萬元,每例輕癥患者平均治療費(fèi)用約為![]() 萬元.根據(jù)(1)中列聯(lián)表數(shù)據(jù),分別求吸煙患者和非吸煙患者的平均治療費(fèi)用.(結(jié)果保留兩位小數(shù))
萬元.根據(jù)(1)中列聯(lián)表數(shù)據(jù),分別求吸煙患者和非吸煙患者的平均治療費(fèi)用.(結(jié)果保留兩位小數(shù))
附:
|
|
|
|
|
|
|
|
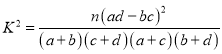
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱柱![]() 平面
平面![]() 是
是![]() 內(nèi)一點(diǎn),點(diǎn)
內(nèi)一點(diǎn),點(diǎn)![]() 在直線
在直線![]() 上運(yùn)動,若直線
上運(yùn)動,若直線![]() 和
和![]() 所成角的最小值與直線
所成角的最小值與直線![]() 和平面
和平面![]() 所成角的最大值相等,則滿足條件的點(diǎn)
所成角的最大值相等,則滿足條件的點(diǎn)![]() 的軌跡是( )
的軌跡是( )
A.直線的一部分B.圓的一部分C.拋物線的一部分D.橢圓的一部分
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
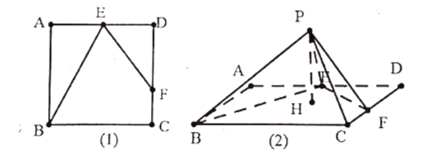
【題目】如圖,邊長為4的正方形![]() ,
,![]() 為
為![]() 中點(diǎn),
中點(diǎn),![]() 為
為![]() 邊上一動點(diǎn),現(xiàn)將
邊上一動點(diǎn),現(xiàn)將![]() ,
,![]() 分別沿
分別沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 重合為點(diǎn)
重合為點(diǎn)![]() ,形成四棱錐
,形成四棱錐![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 平面
平面![]() 于
于![]() .①平面
.①平面![]() 平面
平面![]() ;②當(dāng)
;②當(dāng)![]() 為
為![]() 中點(diǎn)時,三棱錐
中點(diǎn)時,三棱錐![]() 的體積為
的體積為![]() ;③
;③![]() 為
為![]() 的垂心;④
的垂心;④![]() 長的取值范圍為
長的取值范圍為![]() .則以上判斷正確的有______(填正確命題的序號).
.則以上判斷正確的有______(填正確命題的序號).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平行四邊形ABCD中,∠A![]() ,2AB=BC,E,F分別是BC,AD的中點(diǎn).將四邊形DCEF沿著EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
,2AB=BC,E,F分別是BC,AD的中點(diǎn).將四邊形DCEF沿著EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
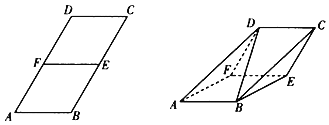
(1)證明:DB⊥EF;
(2)若AB=2,求三棱柱AFD﹣BEC的體積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com