
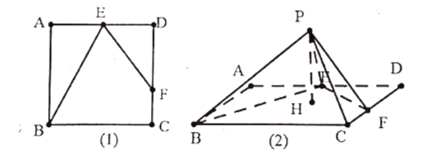
【題目】如圖,邊長為4的正方形![]() ,
,![]() 為
為![]() 中點,
中點,![]() 為
為![]() 邊上一動點,現將
邊上一動點,現將![]() ,
,![]() 分別沿
分別沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 重合為點
重合為點![]() ,形成四棱錐
,形成四棱錐![]() ,過點
,過點![]() 作
作![]() 平面
平面![]() 于
于![]() .①平面
.①平面![]() 平面
平面![]() ;②當
;②當![]() 為
為![]() 中點時,三棱錐
中點時,三棱錐![]() 的體積為
的體積為![]() ;③
;③![]() 為
為![]() 的垂心;④
的垂心;④![]() 長的取值范圍為
長的取值范圍為![]() .則以上判斷正確的有______(填正確命題的序號).
.則以上判斷正確的有______(填正確命題的序號).
 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,已知直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,已知直線![]() 的參數方程為
的參數方程為 ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]()
![]() 求直線
求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
![]() 若把曲線
若把曲線![]() 上給點的橫坐標伸長為原來的
上給點的橫坐標伸長為原來的![]() 倍,縱坐標伸長為原來的
倍,縱坐標伸長為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
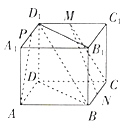
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,M,N,P分別是C1D1,BC,A1D1的中點,有下列四個結論:
①AP與CM是異面直線;②AP,CM,DD1相交于一點;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正確結論的編號是( )
A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,極點為![]() ,一條封閉的曲線
,一條封閉的曲線![]() 由四段曲線組成:
由四段曲線組成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求該封閉曲線所圍成的圖形面積;
(2)若直線![]() :
:![]() 與曲線
與曲線![]() 恰有3個公共點,求
恰有3個公共點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且點
,且點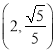 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,在直線
兩點,在直線![]() 上存在點
上存在點![]() ,使三角形
,使三角形![]() 為正三角形,求
為正三角形,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列{an}中,已知a1+a3=12,a2+a4=18,n∈N*.
(1)求數列{an}的通項公式;
(2)求a3+a6+a9+…+a3n.
查看答案和解析>>
科目:高中數學 來源: 題型:
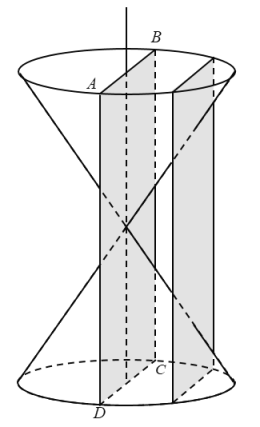
【題目】古希臘數學家阿波羅尼奧斯在他的著作《圓錐曲線論》中記載了用平面切制圓錐得到圓錐曲線的方法.如圖,將兩個完全相同的圓錐對頂放置(兩圓錐的軸重合),已知兩個圓錐的底面半徑為1,母線長均為![]() ,記過圓錐軸的平面ABCD為平面
,記過圓錐軸的平面ABCD為平面![]() (
(![]() 與兩個圓錐面的交線為AC、BD),用平行于
與兩個圓錐面的交線為AC、BD),用平行于![]() 的平面截圓錐,該平面與兩個圓錐側面的截線即為雙曲線E的一部分,且雙曲線E的兩條漸近線分別平行于AC、BD,則雙曲線E的離心率為( )
的平面截圓錐,該平面與兩個圓錐側面的截線即為雙曲線E的一部分,且雙曲線E的兩條漸近線分別平行于AC、BD,則雙曲線E的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com