
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數,
為自然對數的底數,![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)若存在實數![]() ,使得
,使得![]() ,且
,且![]() ,求證:
,求證:![]()
科目:高中數學 來源: 題型:
【題目】如圖,平面ABCD⊥平面CDEF,且四邊形ABCD是梯形,四邊形CDEF是矩形,![]()
![]() ,M是線段DE上的點,滿足DM=2ME.
,M是線段DE上的點,滿足DM=2ME.
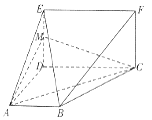
(1)證明:BE//平面MAC;
(2)求直線BF與平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),圓
為參數),圓![]() 的方程為
的方程為![]() .以原點
.以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(Ⅰ)求直線![]() 及圓
及圓![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著互聯網的興起,越來越多的人選擇網上購物.某購物平臺為了吸引顧客,提升銷售額,每年雙十一都會進行某種商品的促銷活動.該商品促銷活動規則如下:①“價由客定”,即所有參與該商品促銷活動的人進行網絡報價,每個人并不知曉其他人的報價,也不知道參與該商品促銷活動的總人數;②報價時間截止后,系統根據當年雙十一該商品數量配額,按照參與該商品促銷活動人員的報價從高到低分配名額;③每人限購一件,且參與人員分配到名額時必須購買.某位顧客擬參加2019雙十一該商品促銷活動,他為了預測該商品最低成交價,根據該購物平臺的公告,統計了最近5年雙十一參與該商品促銷活動的人數(見下表)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份編號t | 1 | 2 | 3 | 4 | 5 |
參與人數(百萬人) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集數據的散點圖發現,可用線性回歸模型模擬擬合參與人數![]() (百萬人)與年份編號
(百萬人)與年份編號![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程:
的線性回歸方程:![]() ,并預測2019年雙十一參與該商品促銷活動的人數;
,并預測2019年雙十一參與該商品促銷活動的人數;
(2)該購物平臺調研部門對2000位擬參與2019年雙十一該商品促銷活動人員的報價價格進行了一個抽樣調查,得到如下的一份頻數表:
報價區間(千元) |
|
|
|
|
|
|
頻數 | 200 | 600 | 600 | 300 | 200 | 100 |
①求這2000為參與人員報價![]() 的平均值
的平均值![]() 和樣本方差
和樣本方差![]() (同一區間的報價可用該價格區間的中點值代替);
(同一區間的報價可用該價格區間的中點值代替);
②假設所有參與該商品促銷活動人員的報價![]() 可視為服從正態分布
可視為服從正態分布![]() ,且
,且![]() 與
與![]() 可分別由①中所求的樣本平均值
可分別由①中所求的樣本平均值![]() 和樣本方差
和樣本方差![]() 估值.若預計2019年雙十一該商品最終銷售量為317400,請你合理預測(需說明理由)該商品的最低成交價.
估值.若預計2019年雙十一該商品最終銷售量為317400,請你合理預測(需說明理由)該商品的最低成交價.
參考公式即數據(i)回歸方程:![]() ,其中
,其中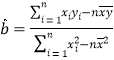 ,
,![]()
(ii)![]()
(iii)若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從1到9的九個數字中取三個偶數四個奇數,試問:
(1)能組成多少個沒有重復數字的七位數?
(2)在(1)中的七位數中三個偶數排在一起的有幾個?
(3)在(1)中的七位數中,偶數排在一起、奇數也排在一起的有幾個?
(4)在(1)中任意兩偶然都不相鄰的七位數有幾個?
(答題要求:先列式,后計算 , 結果用具體數字表示.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]()
![]() R.
R.
(1)如果曲線![]() 在x=1處的切線斜率為1,求實數
在x=1處的切線斜率為1,求實數![]() 的值;
的值;
(2)若函數![]() 的極小值不超過
的極小值不超過![]() ,求實數
,求實數![]() 的最小值;
的最小值;
(3)對任意![]() [1,2],總存在
[1,2],總存在![]() [4,8],使得
[4,8],使得![]() =
=![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值衡量,質量指標值越大表明質量越好,現用一種新配方做試驗,生產了100件這種產品,并測量了每件產品的質量指標值,得到下面試驗結果:
質量指標值 |
|
|
|
|
|
頻數 | 6 | 26 | 38 | 22 | 8 |
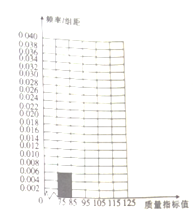
(1)將答題卡上列出的這些數據的頻率分布表填寫完整,并補齊頻率分布直方圖;
(2)估計這種產品質量指標值的平均值(同一組中的數據用該組區間的中點值作代表)與中位數(結果精確到0.1).
質量指標值分組 | 頻數 | 頻率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合計 | 100 | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com