
已知函數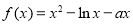 ,
,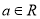 .
.
(1)當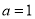 時,求
時,求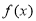 的最小值;
的最小值;
(2)若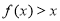 ,求a的取值范圍.
,求a的取值范圍.
(1)0;(2)(-∞,0).
【解析】
試題分析:本題主要考查導數的計算、利用導數判斷函數的單調性、利用導數求函數的最值、恒成立問題等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,對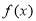 求導,利用“
求導,利用“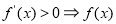 單調遞增,
單調遞增,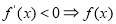 單調遞減”判斷函數的單調性,確定函數最值的位置,并求出函數的最小值;第二問,先將已知不等式進行轉化,將所求的參數分離出來,構造新的函數,利用“
單調遞減”判斷函數的單調性,確定函數最值的位置,并求出函數的最小值;第二問,先將已知不等式進行轉化,將所求的參數分離出來,構造新的函數,利用“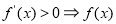 單調遞增,
單調遞增,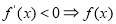 單調遞減”判斷函數的單調性,確定函數最值的位置,并求出函數的最值,代入到所轉化的式子中即可.
單調遞減”判斷函數的單調性,確定函數最值的位置,并求出函數的最值,代入到所轉化的式子中即可.
試題解析:(1)當a=1時,f(x)=x2-lnx-x,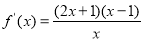 .
.
當x∈(0,1)時,f?(x)<0;當x∈(1,+∞)時,f?(x)>0.
所以f(x)的最小值為f(1)=0. 5分
(2)f(x)>x,即f(x)-x=x2-lnx-(a+1)x>0.
由于x>0,所以f(x)>x等價于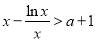 . 7分
. 7分
令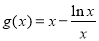 ,則
,則 .
.
當x∈(0,1)時,g?(x)<0;當x∈(1,+∞)時,g?(x)>0.
g(x)有最小值g(1)=1.
故a+1<1,a的取值范圍是(-∞,0). 12分
考點:導數的計算、利用導數判斷函數的單調性、利用導數求函數的最值、恒成立問題.


科目:高中數學 來源:2013-2014學年河北省石家莊市畢業班第一次模擬考試數學理科數學試卷(解析版) 題型:解答題
如圖,在三棱柱 中,
中, ,頂點
,頂點 在底面
在底面 上的射影恰為點
上的射影恰為點 ,
, .
.
(1)證明:平面 平面
平面 ;
;
(2 )若點 為
為 的中點,求出二面角
的中點,求出二面角 的余弦值.
的余弦值.

(1)證明:平面 平面
平面 ;
;
(2)若點 為
為 的中點,求出二面角
的中點,求出二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省石家莊市畢業班第一次模擬考試數學理文數學試卷(解析版) 題型:選擇題
已知i為虛數單位,a∈R,若(a-1)(a+1+i)=a2-1+(a-1)i是純虛數,則a的值為()
A.-1或1
B.1
C.3
D.-1
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省唐山市高三年級第二次模擬考試理科數學試卷(解析版) 題型:選擇題
直三棱柱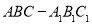 的所有頂點都在半徑為
的所有頂點都在半徑為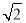 的球面上,
的球面上,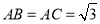 ,
,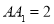 ,則二面角
,則二面角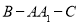 的余弦值為( )
的余弦值為( )
A.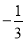 B.
B.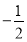 C.
C.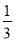 D.
D.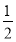
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省唐山市高三年級第二次模擬考試文科數學試卷(解析版) 題型:選擇題
正三棱柱的底面邊長為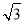 ,高為2,則直三棱柱的外接球的表面積為( )
,高為2,則直三棱柱的外接球的表面積為( )
A.  B.
B. 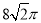 C.
C. 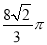 D.
D. 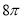
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省高三下學期調研考試理科數學試卷(解析版) 題型:解答題
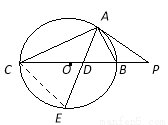
如圖, 是⊙
是⊙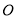 的直徑,
的直徑,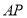 是⊙
是⊙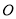 的切線,
的切線,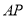 與
與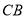 的延長線交于點
的延長線交于點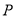 ,
,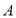 為切點.若
為切點.若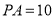 ,
,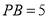 ,
,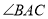 的平分線
的平分線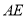 與
與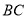 和⊙
和⊙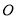 分別交于點
分別交于點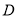 、
、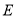 ,求
,求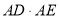 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com