
| A. | 4條 | B. | 3條 | C. | 2條 | D. | 1條 |
分析 將兩圓化成標準方程,可得它們的圓心坐標和半徑大小,從而得到兩圓的圓心距等于13,恰好介于兩圓的半徑差與半徑和之間,由此可得兩圓位置關系是相交,從而得到它們有兩條公切線.
解答 解:∵圓C1:x2+y2-6x+16y-48=0化成標準方程,得(x-3)2+(y+8)2=121
∴圓C1的圓心坐標為(3,-8),半徑r1=11
同理,可得圓C2的圓心坐標為(-2,4),半徑r2=8
因此,兩圓的圓心距|C1C2|=$\sqrt{(3+2)^{2}+(-8-4)^{2}}$=13
∵|r1-r2|<|C1C2|<r1+r2=16
∴兩圓的位置關系是相交,可得兩圓有2條公切線
故選:C
點評 本題給出兩個圓的一般式方程,探求兩圓的位置關系并找出公切線的條數,著重考查了圓的一般式方程與標準方程的互化和兩圓位置關系的判斷等知識點,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | 2i∈P | B. | $\frac{2}{i}$∈P | C. | ($\sqrt{2}$i)2∈P | D. | $\frac{2}{{i}^{3}}$∈P |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | tan$\frac{4π}{7}$>tan$\frac{3π}{7}$ | B. | tan$\frac{2π}{5}$<tan$\frac{3π}{5}$ | ||
| C. | tan(-$\frac{13π}{7}$)>tan(-$\frac{15π}{8}$) | D. | tan(-$\frac{13π}{4}$)<tan(-$\frac{12π}{5}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
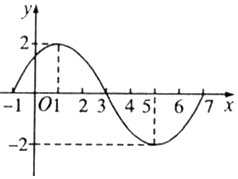 已知函數y=Asin(ωx+φ)(A>0,ω>0)在一個周期內的圖象如圖所示.
已知函數y=Asin(ωx+φ)(A>0,ω>0)在一個周期內的圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com