
分析 (1)求出原函數的導函數,由導函數大于0求得函數的增區間,由導函數小于0求得函數的減區間,進一步得到函數的極大值;
(2)求出g(x),構造函數h(x)=f(x)-g(x),求導可知函數g(x)在(3,+∞)上為增函數,由h(x)>h(3)證得結論.
解答 解:(1)f′(x)$\frac{{e}^{x}-(x-2){e}^{x}}{{e}^{2x}}$=$\frac{3-x}{{e}^{x}}$,
令f′(x)>0,解得:x<3,
令f′(x)<0,解得:x>3,
故f(x)在(-∞,3)遞增,在(3,+∞)遞減,
故f(x)極大值=f(3)=$\frac{1}{{e}^{3}}$;
證明:(2)g(x)=f(6-x)=$\frac{4-x}{{e}^{6-x}}$,
令h(x)=f(x)-g(x)=$\frac{x-2}{{e}^{x}}$-$\frac{4-x}{{e}^{6-x}}$,(x>3),
則h′(x)=$\frac{3-x}{{e}^{x}}$$-\frac{3-x}{{e}^{6-x}}$=$(3-x)(\frac{1}{{e}^{x}}-\frac{1}{{e}^{6-x}})$.
當x>3時,x>6-x,ex>e6-x>0,則$\frac{1}{{e}^{x}}$<$\frac{1}{{e}^{6-x}}$.
∴h′(x)>0,函數h(x)在(3,+∞)上為增函數,
則h(x)>h(3)=$\frac{3-2}{{e}^{3}}-\frac{4-3}{{e}^{3}}=0$.
∴當x>3時,f(x)>g(x).
點評 本題考查利用導數研究函數的單調性,訓練了利用導數證明函數不等式的方法,是中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
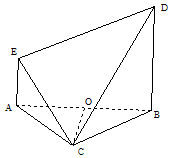 如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.
如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-2,-1,1,2} | B. | {-1,1} | C. | {2} | D. | {1} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com