
【題目】已知①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 在如右圖所示的程序框圖中,如果輸入
在如右圖所示的程序框圖中,如果輸入![]() ,而輸出
,而輸出![]() ,則在空白處可填入( )
,則在空白處可填入( )
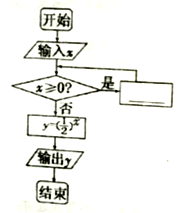
A.①②③ B.②③ C.③④ D.②③④
【答案】D
【解析】
試題:①若填入![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
…
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,不滿足進行循環的條件,
時,不滿足進行循環的條件,
此時輸出![]() ,不滿足題目要求;
,不滿足題目要求;
②若填入![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,不滿足進行循環的條件,
時,不滿足進行循環的條件,
此時輸出![]() ,滿足題目要求;
,滿足題目要求;
③若填入![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件
時,滿足進行循環的條件![]() ,,
,,
當![]() 時,不滿足進行循環的條件,
時,不滿足進行循環的條件,
此時輸出![]() ,滿足題目要求;
,滿足題目要求;
④若填入![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,滿足進行循環的條件,
時,滿足進行循環的條件,![]() ,
,
當![]() 時,不滿足進行循環的條件,
時,不滿足進行循環的條件,
此時輸出![]() ,滿足題目要求;
,滿足題目要求;
綜上所述,圖中“?”處可填入的算法語句是②③④,
故答案為:②③④


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
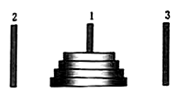
【題目】如圖所示,有三根針和套在一根針上的![]() 個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
(1)每次只能移動一個金屬片;
(2)在每次移動過程中,每根針上較大的金屬片不能放在較小的金屬片上面.
將![]() 個金屬片從1號針移到3號針最少需要移動的次數記為
個金屬片從1號針移到3號針最少需要移動的次數記為![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為確定下一年度投入某種產品的生產所需的資金,需了解每投入2千萬資金后,工人人數![]() (單位:百人)對年產能
(單位:百人)對年產能![]() (單位:千萬元)的影響,對投入的人力和年產能的數據作了初步處理,得到散點圖和統計量表.
(單位:千萬元)的影響,對投入的人力和年產能的數據作了初步處理,得到散點圖和統計量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
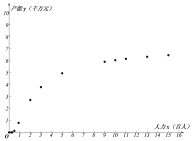
(1)根據散點圖判斷:![]() 與
與![]() 哪一個適宜作為年產能
哪一個適宜作為年產能![]() 關于投入的人力
關于投入的人力![]() 的回歸方程類型?并說明理由?
的回歸方程類型?并說明理由?
(2)根據(1)的判斷結果及相關的計算數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)現該企業共有2000名生產工人,資金非常充足,為了使得年產能達到最大值,則下一年度共需投入多少資金(單位:千萬元)?
附注:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為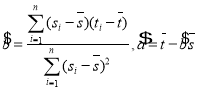 ,(說明:
,(說明:![]() 的導函數為
的導函數為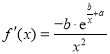 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位所著,該作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉變,該作中有題為“李白沽酒”“李白街上走,提壺去買酒。遇店加一倍,見花喝一斗,三遇店和花,喝光壺中酒。借問此壺中,原有多少酒?”,如圖為該問題的程序框圖,若輸出的![]() 值為0,則開始輸入的
值為0,則開始輸入的![]() 值為( )
值為( )
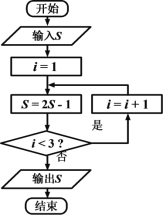
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等腰直角三角形![]() 的斜邊AB為正四面體
的斜邊AB為正四面體![]() 側棱,直角邊AE繞斜邊AB旋轉,則在旋轉的過程中,有下列說法:
側棱,直角邊AE繞斜邊AB旋轉,則在旋轉的過程中,有下列說法:

(1)四面體E![]() BCD的體積有最大值和最小值;
BCD的體積有最大值和最小值;
(2)存在某個位置,使得![]() ;
;
(3)設二面角![]() 的平面角為
的平面角為![]() ,則
,則![]() ;
;
(4)AE的中點M與AB的中點N連線交平面BCD于點P,則點P的軌跡為橢圓.
其中,正確說法的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,直線
中,直線![]() 經過點
經過點![]() ,傾斜角為
,傾斜角為![]() ,以原點為極點,
,以原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為曲線
的極坐標方程為曲線![]() .
.
(Ⅰ)寫出直線![]() 的參數方程及曲線
的參數方程及曲線![]() 的普通方程;
的普通方程;
(Ⅱ)求直線![]() 和曲線
和曲線![]() 的兩個交點到點
的兩個交點到點![]() 的距離的和與積.
的距離的和與積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2016年1月至2018年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.
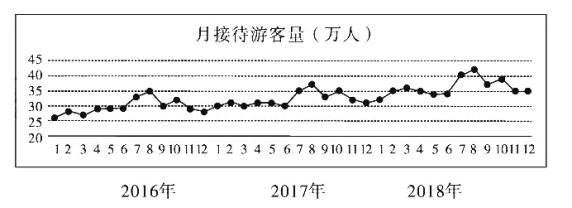
根據該折線圖,判斷下列結論:
(1)月接待游客量逐月增加;
(2)年接待游客量逐年增加;
(3)各年的月接待游客量高峰期大致在7,8月;
(4)各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩.
其中正確結論的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 、
、![]() 是兩個相交平面,則在下列命題中,真命題的序號為( )
是兩個相交平面,則在下列命題中,真命題的序號為( )
①若直線![]() ,則在平面
,則在平面![]() 內一定不存在與直線
內一定不存在與直線![]() 平行的直線.
平行的直線.
②若直線![]() ,則在平面
,則在平面![]() 內一定存在無數條直線與直線
內一定存在無數條直線與直線![]() 垂直.
垂直.
③若直線![]() ,則在平面
,則在平面![]() 內不一定存在與直線
內不一定存在與直線![]() 垂直的直線.
垂直的直線.
④若直線![]() ,則在平面
,則在平面![]() 內一定存在與直線
內一定存在與直線![]() 垂直的直線.
垂直的直線.
A. ①③ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為2,離心率為
的短軸長為2,離心率為![]() ,
,![]() ,
,![]() 分別是橢圓的右頂點和下頂點.
分別是橢圓的右頂點和下頂點.
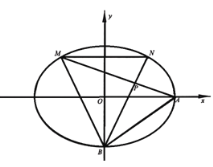
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知![]() 是橢圓
是橢圓![]() 內一點,直線
內一點,直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,直線
,直線![]() 分別交橢圓于
分別交橢圓于![]() 兩點,記
兩點,記![]() ,
,![]() 的面積分別為
的面積分別為![]() ,
,![]() .
.
①若![]() 兩點關于
兩點關于![]() 軸對稱,求直線
軸對稱,求直線![]() 的斜率;
的斜率;
②證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com