
【題目】為了研究某種微生物的生長規(guī)律,研究小組在實驗室對該種微生物進行培育實驗.前三天觀測的該微生物的群落單位數(shù)量分別為12,16,24.根據(jù)實驗數(shù)據(jù),用y表示第![]() 天的群落單位數(shù)量,某研究員提出了兩種函數(shù)模型;①
天的群落單位數(shù)量,某研究員提出了兩種函數(shù)模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常數(shù).
,其中a,b,c,p,q,r都是常數(shù).
(1)根據(jù)實驗數(shù)據(jù),分別求出這兩種函數(shù)模型的解析式;
(2)若第4天和第5天觀測的群落單位數(shù)量分別為40和72,請從這兩個函數(shù)模型中選出更合適的一個,并計算從第幾天開始該微生物群落的單位數(shù)量超過1000.
【答案】(1)函數(shù)模型:①![]() ;函數(shù)模型②:
;函數(shù)模型②:![]() (2)函數(shù)模型②更合適;從第9天開始該微生物群落的單位數(shù)量超過1000
(2)函數(shù)模型②更合適;從第9天開始該微生物群落的單位數(shù)量超過1000
【解析】
(1)由題意利用待定系數(shù)法求函數(shù)的解析式;
(2)將![]() ,
,![]() 代入(1)中的兩個函數(shù)解析式中,結合數(shù)據(jù)判斷兩個模型中那個更合適。
代入(1)中的兩個函數(shù)解析式中,結合數(shù)據(jù)判斷兩個模型中那個更合適。
(1)由題意,對于函數(shù)模型①:把![]() 代入
代入![]() 得
得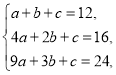
解得![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
對于函數(shù)模型②:把![]() 代入
代入![]() 得
得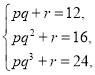
解得![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
(2)將![]() ,
,![]() 代入函數(shù)模型①,得
代入函數(shù)模型①,得![]() ,
,![]() ,不符合觀測數(shù)據(jù);
,不符合觀測數(shù)據(jù);
將![]() ,
,![]() 代入函數(shù)模型②,得
代入函數(shù)模型②,得![]() ,
,![]() ,符合觀測數(shù)據(jù).
,符合觀測數(shù)據(jù).
所以函數(shù)模型②更合適.
令![]() ,因為
,因為![]() ,可得
,可得![]() ,
,
即從第9天開始該微生物群落的單位數(shù)量超過1000.


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數(shù)學 來源: 題型:
【題目】中國古代名詞“芻童”原來是草堆的意思,關于“芻童”體積計算的描述,《九章算術》注曰:“倍上袤,下袤從之,亦倍下袤,上袤從之,各以其廣乘之,并,以高乘之,皆六而一.”其計算方法是:將上底面的長乘二,與下底面的長相加,再與上底面的寬相乘,將下底面的長乘二,與上底面的長相加,再與下底面的寬相乘;把這兩個數(shù)值相加,與高相乘,再取其六分之一.已知一個“芻童”的下底面是周長為18的矩形,上底面矩形的長為3,寬為2,“芻童”的高為3,則該“芻童”的體積的最大值為
A. ![]() B.
B. ![]() C. 39 D.
C. 39 D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司計劃投資A、B兩種金融產(chǎn)品,根據(jù)市場調查與預測,A產(chǎn)品的利潤與投資量成正比例,其關系如圖1,B產(chǎn)品的利潤與投資量的算術平方根成正比例,其關系如圖2(注:利潤與投資量的單位:萬元).
(1)分別將A、B兩產(chǎn)品的利潤表示為投資量的函數(shù)關系式;
(2)該公司已有10萬元資金,并全部投入A、B兩種產(chǎn)品中,問:怎樣分配這10萬元投資,才能使公司獲得最大利潤?其最大利潤為多少萬元?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓![]() ,其中
,其中![]() ,焦距為2,過點
,焦距為2,過點![]() 的直線l與橢圓C交于點A,B,點B在A,M之間.又線段AB的中點的橫坐標為
的直線l與橢圓C交于點A,B,點B在A,M之間.又線段AB的中點的橫坐標為![]() ,且
,且![]() .
.
(1)求橢圓C的標準方程.
(2)求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() .當
.當![]() 軸時,
軸時,![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是偶函數(shù).
是偶函數(shù).
(1)求實數(shù)![]() 的值;
的值;
(2)若![]() 的圖像在直線
的圖像在直線![]() 下方,求b的取值范圍;
下方,求b的取值范圍;
(3)設函數(shù)![]() ,若
,若![]() 在
在![]() 上的最小值為0,求實數(shù)m的值.
上的最小值為0,求實數(shù)m的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來“雙十一”已成為中國電子商務行業(yè)的年度盛事,并且逐漸影響到國際電子商務行業(yè).某商家為了準備2018年雙十一的廣告策略,隨機調查1000名淘寶客戶在2017年雙十一前后10天內網(wǎng)購所花時間,并將調查結果繪制成如圖所示的頻率分布直方圖.

由頻率分布直方圖可以認為,這10天網(wǎng)購所花的時間![]() 近似服從
近似服從![]() ,其中
,其中![]() 用樣本平均值代替,
用樣本平均值代替,![]() .
.
(Ⅰ)計算樣本的平均值![]() ,并利用該正態(tài)分布求
,并利用該正態(tài)分布求![]() .
.
(Ⅱ)利用由樣本統(tǒng)計獲得的正態(tài)分布估計整體,將這10天網(wǎng)購所花時間在![]() 小時內的人定義為目標客戶,對目標客戶發(fā)送廣告提醒.現(xiàn)若隨機抽取10000名淘寶客戶,記
小時內的人定義為目標客戶,對目標客戶發(fā)送廣告提醒.現(xiàn)若隨機抽取10000名淘寶客戶,記![]() 為這10000人中目標客戶的人數(shù).
為這10000人中目標客戶的人數(shù).
(i)求![]() ;
;
(ii)問:10000人中目標客戶的人數(shù)![]() 為何值的概率最大?
為何值的概率最大?
附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如下圖所示,在三棱錐P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,點D,E分別在棱PB,PC上,且DE∥BC.

(1)求證:BC⊥平面PAC;
(2)當D為PB的中點時,求AD與平面PAC所成的角的正弦值;
(3)是否存在點E,使得二面角A-DE-P為直二面角?并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】經(jīng)市場調查,某超市的一種商品在過去的一個月內(以30天計算),銷售價格![]() 與時間(天)的函數(shù)關系近似滿足
與時間(天)的函數(shù)關系近似滿足![]() ,銷售量
,銷售量![]() 與時間(天)的函數(shù)關系近似滿足
與時間(天)的函數(shù)關系近似滿足 .
.
(1)試寫出該商品日銷售金額![]() 關于時間
關于時間![]() 的函數(shù)表達式;
的函數(shù)表達式;
(2)求該商品的日銷售金額![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com