
【題目】已知函數![]() 是偶函數.
是偶函數.
(1)求實數![]() 的值;
的值;
(2)若![]() 的圖像在直線
的圖像在直線![]() 下方,求b的取值范圍;
下方,求b的取值范圍;
(3)設函數![]() ,若
,若![]() 在
在![]() 上的最小值為0,求實數m的值.
上的最小值為0,求實數m的值.
 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界.已知函數
的上界.已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的值域,并判斷函數
上的值域,并判斷函數![]() 在
在![]() 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若![]() 是
是![]() 上的有界函數,且
上的有界函數,且![]() 的上界為3,求實數
的上界為3,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河南濮陽市高三一模】已知點![]() 在拋物線
在拋物線![]() 上,
上, ![]() 是拋物線上異于
是拋物線上異于![]() 的兩點,以
的兩點,以![]() 為直徑的圓過點
為直徑的圓過點![]() .
.
(I)證明:直線![]() 過定點;
過定點;
(II)過點![]() 作直線
作直線![]() 的垂線,求垂足
的垂線,求垂足![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究某種微生物的生長規律,研究小組在實驗室對該種微生物進行培育實驗.前三天觀測的該微生物的群落單位數量分別為12,16,24.根據實驗數據,用y表示第![]() 天的群落單位數量,某研究員提出了兩種函數模型;①
天的群落單位數量,某研究員提出了兩種函數模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常數.
,其中a,b,c,p,q,r都是常數.
(1)根據實驗數據,分別求出這兩種函數模型的解析式;
(2)若第4天和第5天觀測的群落單位數量分別為40和72,請從這兩個函數模型中選出更合適的一個,并計算從第幾天開始該微生物群落的單位數量超過1000.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程是
的參數方程是 (
(![]() 是參數),圓
是參數),圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求圓心![]() 的直角坐標;
的直角坐標;
(Ⅱ)由直線![]() 上的點向圓
上的點向圓![]() 引切線,求切線長的最小值.
引切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程是
的參數方程是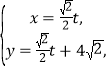 (
(![]() 是參數),圓
是參數),圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求圓心![]() 的直角坐標;
的直角坐標;
(Ⅱ)由直線![]() 上的點向圓
上的點向圓![]() 引切線,求切線長的最小值.
引切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中![]() 中,直線
中,直線![]() ,圓
,圓![]() 的參數方程為
的參數方程為![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求直線![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com