
【題目】已知橢圓![]() 的離心率
的離心率![]() ,過點
,過點![]() 和
和![]() 的直線與原點的距離為
的直線與原點的距離為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,過
的左、右焦點,過![]() 作直線交橢圓于
作直線交橢圓于![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)先求出直線![]() 方程為
方程為![]() ,利用原點到直線的距離建立方程并化簡得
,利用原點到直線的距離建立方程并化簡得![]() ,有離心率
,有離心率![]() 及
及![]() ,解方程組求得:
,解方程組求得:![]() ,故橢圓方程為
,故橢圓方程為![]() ;(2)設直線
;(2)設直線![]() 的方程為:
的方程為:![]() ,聯立直線與橢圓方程,寫出根與系數關系,利用弦長公式求得
,聯立直線與橢圓方程,寫出根與系數關系,利用弦長公式求得![]() 面積的表達式,利用基本不等式求得最大值為
面積的表達式,利用基本不等式求得最大值為![]() .
.
試題解析:
(1)直線![]() 的方程為
的方程為![]() 即
即![]() ,
,
原點到直線![]() 的距離為
的距離為![]() 即
即![]() .............①
.............①
![]() ...........②
...........②
又![]() ..........③
..........③
由①②③可得:![]() 故橢圓方程為
故橢圓方程為![]() ;
;
(2)![]() ,設
,設![]() ,
,
由于直線![]() 的斜率不為0,故設其方程為:
的斜率不為0,故設其方程為:![]() ,
,
聯立直線與橢圓方程:
 或
或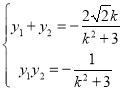 ..........④
..........④
![]() ................⑤
................⑤
將④代入⑤得: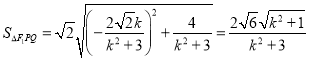 ,
,
令![]() ,則
,則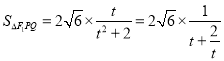 ,
,
當且僅當![]() ,即
,即![]() ,即
,即![]() 時,
時,![]() 面積取最大值
面積取最大值![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,圓錐頂點為![]() ,底面圓心為
,底面圓心為![]() ,其母線與底面所成的角為45°,
,其母線與底面所成的角為45°,![]() 和
和![]() 是底面圓
是底面圓![]() 上的兩條平行的弦,
上的兩條平行的弦,![]() .
.

(1)證明:平面![]() 與平面
與平面![]() 的交線平行于底面;
的交線平行于底面;
(2)求軸![]() 與平面
與平面![]() 所成的角的正切值.
所成的角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線l經過第二、三、四象限,則直線l的傾斜角的范圍是 ( )
A. 0°≤α<90° B. 90°≤α<180°
C. 90°<α<180° D. 0°≤α<180°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右頂點為
的左右頂點為![]() 、
、![]() ,左右焦點為
,左右焦點為![]() ,其長半軸的長等于焦距,點
,其長半軸的長等于焦距,點![]() 是橢圓上的動點,
是橢圓上的動點,![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓的方程;
(2)設![]() 為直線
為直線![]() 上不同于點
上不同于點![]() 的任意一點,若直線
的任意一點,若直線![]() 、
、![]() 分別與橢圓交于異于
分別與橢圓交于異于![]() 、
、![]() 的點
的點![]() 、
、![]() ,判斷點
,判斷點![]() 與以
與以![]() 為直徑的圓的位置關系.
為直徑的圓的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】育才高中為了推進新課程改革,滿足不同層次學生的需求,決定在每周的周一、周三、周五的課外活動期間同時開設“茶藝”、“模擬駕駛”、“機器人制作”、“數學與生活”和“生物與環境”選修課,每位有興趣的同學可以在任何一天參加任何一門科目.(規定:各科達到預先設定的人數時稱為滿座,否則稱為不滿座)統計數據表明,各選修課各天的滿座的概率如下表:
生物與環境 | 數學與生活 | 機器人制作 | 模擬駕駛 | 茶藝 | |
周一 |
|
|
|
|
|
周三 |
|
|
|
|
|
周五 |
|
|
|
|
|
(1)求茶藝選修課在周一、周三、周五都不滿座的概率;
(2)設周三各選修課中滿座的科目數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,函數
,函數![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直.
垂直.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)若函數![]() 存在單調遞減區間,求實數
存在單調遞減區間,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)設![]() 是函數
是函數![]() 的兩個極值點,若
的兩個極值點,若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在(﹣1,1)上的奇函數f(x),在x∈(﹣1,0)時,f(x)=2x+2﹣x.
(1)求f(x)在(﹣1,1)上的表達式;
(2)用定義證明f(x)在(﹣1,0)上是減函數;
(3)若對于x∈(0,1)上的每一個值,不等式m2xf(x)<4x﹣1恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com