
(本小題滿分12分)
如圖,飛機的航線和山頂在同一個鉛直平面內,已知飛機的高度為海拔25000米,速度為3000米/分鐘,飛行員先在點A看到山頂C的俯角為300,經過8分鐘后到達點B,此時看到山頂C的俯角為600,則山頂的海拔高度為多少米.(參考數據: =1.414,
=1.414, =1.732,
=1.732, =2.449).
=2.449).
4216
解析試題分析:如圖,過C作AB的垂線,垂足為D,  依題意,AB=3000·8=24000米,
依題意,AB=3000·8=24000米,
由∠BAC=300,∠DBC=600,則∠BCA=300,∴ BC=24000米, 在直角三角形CBD中,
CD=BC·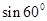 =24000·0.866=20784米,
=24000·0.866=20784米,
故山頂的海拔高度為25000-20784=4216米.
考點:本題考查了正余弦定理的實際運用
點評:正余弦定理在測量、航海、物理、幾何、天體運行等方面的應用十分廣泛,解這類應用題需要我們吃透題意,對專業名詞、術語要能正確理解,能將實際問題歸結為數學問題.求解此類問題的大概步驟為:(1)準確理解題意,分清已知與所求,準確理解應用題中的有關名稱、術語,如仰角、俯角、視角、象限角、方位角等;(2)根據題意畫出圖形;(3)將要求解的問題歸結到一個或幾個三角形中,通過合理運用正弦定理、余弦定理等有關知識建立數學模型,然后正確求解,演算過程要簡練,計算要準確,最后作答


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com