
【題目】設![]() ,函數
,函數![]() ,
,![]() .已知
.已知![]() 的最小正周期為
的最小正周期為![]() ,且
,且![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)求![]() 的單調遞增區間;
的單調遞增區間;
(3)求函數![]() 在區間
在區間![]() 上的最小值和最大值.
上的最小值和最大值.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】某村計劃建造一個室內面積為800![]() 的矩形蔬菜溫室.在溫室內,沿左右兩側與后側內墻各保留1
的矩形蔬菜溫室.在溫室內,沿左右兩側與后側內墻各保留1![]() 寬的通道,沿前側內墻保留3
寬的通道,沿前側內墻保留3![]() 寬的空地.當矩形溫室的邊長各為多少時?蔬菜的種植面積最大,最大種植面積是多少?
寬的空地.當矩形溫室的邊長各為多少時?蔬菜的種植面積最大,最大種植面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐P-A BC的四個頂點都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA =3,AB=BC=2,則球O的表面積為( )
A.13π B.17π C.52π D.68π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C、F是⊙O上的兩點,OC⊥AB,過點F作⊙O的切線FD交AB的延長線于點D.連接CF交AB于點E.
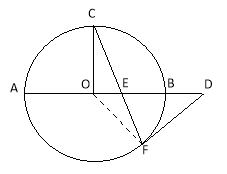
(1)求證:DE2=DBDA;
(2)若DB=2,DF=4,試求CE的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 為圓
為圓![]() 上的動點,定點
上的動點,定點![]() ,線段
,線段![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點
于點![]() .
.
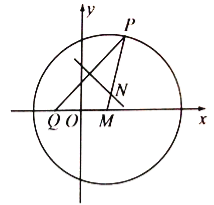
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)記動點![]() 的軌跡為曲線
的軌跡為曲線 ![]() ,設圓
,設圓![]() 的切線
的切線![]() 交曲線
交曲線![]() 于
于![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓的四個頂點為頂點的四邊形的面積為
,以橢圓的四個頂點為頂點的四邊形的面積為![]() .
.
(1)求橢圓的方程;
(2)斜率為![]() 的直線
的直線![]() 過橢圓的右焦點
過橢圓的右焦點![]() ,且與橢圓交與
,且與橢圓交與![]() 兩點,過線段
兩點,過線段![]() 的中點與
的中點與![]() 垂直的直線交直線
垂直的直線交直線![]() 于
于![]() 點,若
點,若![]() 為等邊三角形,求直線
為等邊三角形,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“銀發浪潮”的涌來,養老是當下普遍關注的熱點和難點問題,某市創新性的采用“公建民營”的模式,建立標準的“日間照料中心”,既吸引社會力量廣泛參與養老建設,也方便規范化管理,計劃從中抽取5個中心進行評估,現將所有中心隨機編號,用系統(等距)抽樣的方法抽取,已知抽取到的號碼有5號23號和29號,則下面號碼中可能被抽到的號碼是( )
A. 9 B. 12 C. 15 D. 17
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為2萬元,并且每生產1百臺的生產成本為1萬元(總成本
(萬元),其中固定成本為2萬元,并且每生產1百臺的生產成本為1萬元(總成本![]() 固定成本+生產成本),銷售收入
固定成本+生產成本),銷售收入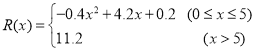 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題
(1)寫出利潤函數![]() 的解析式(利潤
的解析式(利潤![]() 銷售收入—總成本);
銷售收入—總成本);
(2)甲廠生產多少臺新產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國人口已經出現老齡化與少子化并存的結構特征,測算顯示中國是世界上人口老齡化速度最快的國家之一,再不實施“放開二胎”新政策,整個社會將會出現一系列的問題,若某地區2015年人口總數為![]() 萬,實施“放開二胎”新政策后專家估計人口總數將發生如下變化:從2016年開始到2025年每年人口比上年增加
萬,實施“放開二胎”新政策后專家估計人口總數將發生如下變化:從2016年開始到2025年每年人口比上年增加![]() 萬人,從2026年開始到2035年每年人口為上一年的
萬人,從2026年開始到2035年每年人口為上一年的![]() .
.
(1)求實施新政策后第![]() 年的人口總數
年的人口總數![]() 的表達式(注:2016年為第一年);
的表達式(注:2016年為第一年);
(2)若新政策實施后的2016年到2035年人口平均值超過![]() 萬,則需調整政策,否則繼續實施,問到2035年后是否需要調整政策?(說明:
萬,則需調整政策,否則繼續實施,問到2035年后是否需要調整政策?(說明:![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com