
設y=f(x)是定義在區間[-1,1]上的函數,且滿足條件:
(i)f(-1)=f(1)=0;
(ii)對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.
(Ⅰ)證明:對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(Ⅱ)判斷函數g(x)=![]() 是否滿足題設條件;
是否滿足題設條件;
(Ⅲ)在區間[-1,1]上是否存在滿足題設條件的函數y=f(x),且使得對任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|.
若存在,請舉一例;若不存在,請說明理由.
(Ⅰ)證明:由題設條件可得,當x∈[-1,1]時,有 即 (Ⅱ)答:函數g(x)滿足題設條件,驗證如下:g(-1)=0=g(1). 對任意的 當 當 當u·v<0時,不妨設u∈[-1,0],v∈(0,1], 有|g(u)-g(v)|=|(1+u)-(1-v)|=|u+v|≤|v-u|. 所以,函數g(x)滿足題設條件. (Ⅲ)答:這樣的函數不存在.理由如下: 假設存在f(x)滿足條件,則由f(-1)=f(1)=0 , 得| f(1)-f(-1)|=0 ① 由于對任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|, 所以,|f(1)-f(-1)|=|1-(-1)|=2. ② ①與②矛盾,因此假設不成立, 即這樣的函數不存在.
|


科目:高中數學 來源:數學教研室 題型:044
(i)f(-1)=f(1)=0;
(ii)對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.
(Ⅰ)證明:對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(Ⅱ)判斷函數g(x)=![]() 是否滿足題設條件;
是否滿足題設條件;
(Ⅲ)在區間[-1,1]上是否存在滿足題設條件的函數y=f(x),且使得對任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|.
若存在,請舉一例;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2014屆江西贛州會昌中學高二下學期第一次月考理科數學試卷(解析版) 題型:填空題
對于三次函數f(x)=ax3+bx2+cx+d(a≠0),定義:設f″(x)是函數y=f(x)的導數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點 為函數y=f(x)的“拐點”.有同學發現“任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心;且“拐點”就是對稱中心.”請你根據這一發現,請回答問題:
為函數y=f(x)的“拐點”.有同學發現“任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心;且“拐點”就是對稱中心.”請你根據這一發現,請回答問題:
若函數 ,
,
則 = .
= .
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省聊城市高三下學期期初考試文科數學試卷(解析版) 題型:選擇題
對于三次函數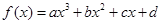 (
(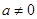 ),定義:設f″(x)是函數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點(x0,f(x0))為函數
),定義:設f″(x)是函數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點(x0,f(x0))為函數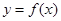 的“拐點”.有同學發現:“任何一個三次函數都有‘拐點’;任何一個三次函數都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發現為條件,若函數
的“拐點”.有同學發現:“任何一個三次函數都有‘拐點’;任何一個三次函數都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發現為條件,若函數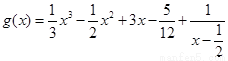 ,則
,則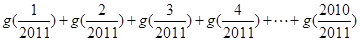 =( )
=( )
A.2010 B.2011 C.2012 D.2013
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省聊城市高三下學期期初考試文科數學試卷(解析版) 題型:選擇題
對于三次函數 (
( ),定義:設f″(x)是函數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點(x0,f(x0))為函數
),定義:設f″(x)是函數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點(x0,f(x0))為函數 的“拐點”.有同學發現:“任何一個三次函數都有‘拐點’;任何一個三次函數都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發現為條件,若函數
的“拐點”.有同學發現:“任何一個三次函數都有‘拐點’;任何一個三次函數都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發現為條件,若函數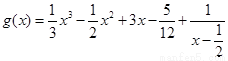 ,則
,則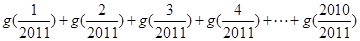 =( )
=( )
A.2010 B.2011 C.2012 D.2013
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com