
【題目】已知點 與點
與點![]() 都在橢圓
都在橢圓![]() 上,且
上,且![]() 的左集點為
的左集點為![]() ,過點
,過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
,![]() 兩點.
兩點.
(1)求![]() 的方程;
的方程;
(2)若以![]() 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)利用點在曲線上,列出方程組求解即可求出橢圓的方程.
(2)依題意可知直線AB的斜率存在,設(shè)為k,則直線AB的方程為![]() ,
,
設(shè)點![]() ,
,![]() .消元列出韋達(dá)定理及判別式,若以AB為直徑的圓經(jīng)過點
.消元列出韋達(dá)定理及判別式,若以AB為直徑的圓經(jīng)過點![]() ,則
,則![]() ,則
,則![]() ,從而計算可得;
,從而計算可得;
解:(1)由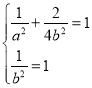 得
得![]() ,
,![]() ,
,
![]() 橢圓C的方程為
橢圓C的方程為![]() .
.
(2)點![]() .顯然直線AB的斜率存在,設(shè)為k,
.顯然直線AB的斜率存在,設(shè)為k,
則直線AB的方程為![]() ,
,
設(shè)點![]() ,
,![]() .
.
聯(lián)立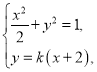 消去y得
消去y得![]() ,
,
故![]() ,
,
所以![]() .(*)
.(*)
且![]() ,
,![]() .
.
所以直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
若以AB為直徑的圓經(jīng)過點![]() ,則
,則![]() .
.
則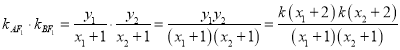
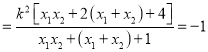 ,
,
得![]() ,
,
則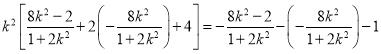 ,
,
化簡得![]() ,解得
,解得![]() .
.
因為![]() 都滿足(*)式,
都滿足(*)式,
所以直線AB的方程為![]() 或
或![]() .
.
即直線AB的方程為![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
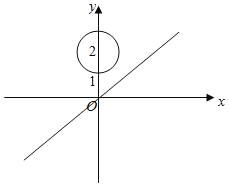
【題目】已知圓![]() 的方程為
的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() ,點
,點![]() 在直線上,過點
在直線上,過點![]() 作圓
作圓![]() 的切線
的切線![]() ,切點為
,切點為![]() .
.
(1)若過點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,求切線
,求切線![]() 方程;
方程;
(2)求四邊形![]() 面積的最小值;
面積的最小值;
(3)求證:經(jīng)過![]() 三點的圓必過定點,并求出所有定點坐標(biāo).
三點的圓必過定點,并求出所有定點坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率是
的離心率是![]() ,短軸的一個端點到右焦點的距離為
,短軸的一個端點到右焦點的距離為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.
兩點.
(1)求橢圓![]() 的方程;
的方程;
(2)當(dāng)實數(shù)![]() 變化時,求
變化時,求![]() 的最大值;
的最大值;
(3)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中,已知曲線C1:![]() (α為參數(shù)),在以O為極點,x軸正半軸為極軸的極坐標(biāo)系中,曲線C2:ρcos
(α為參數(shù)),在以O為極點,x軸正半軸為極軸的極坐標(biāo)系中,曲線C2:ρcos ![]() =-
=-![]() ,曲線C3:ρ=2sin θ.
,曲線C3:ρ=2sin θ.
(1)求曲線C1與C2的交點M的直角坐標(biāo);
(2)設(shè)點A,B分別為曲線C2,C3上的動點,求|AB|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】經(jīng)觀測,某公路段在某時段內(nèi)的車流量![]() (千輛/小時)與汽車的平均速度
(千輛/小時)與汽車的平均速度![]() (千米/小時)之間有函數(shù)關(guān)系:
(千米/小時)之間有函數(shù)關(guān)系:![]() .
.
(1)在該時段內(nèi),當(dāng)汽車的平均速度![]() 為多少時車流量
為多少時車流量![]() 最大?最大車流量為多少?(精確到0.01)
最大?最大車流量為多少?(精確到0.01)
(2)為保證在該時段內(nèi)車流量至少為10千輛/小時,則汽車的平均速度應(yīng)控制在什么范圍內(nèi)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了了解居民的用電情況,某地供電局抽查了該市若干戶居民月均用電量(單位:![]() ),并將樣本數(shù)據(jù)分組為
),并將樣本數(shù)據(jù)分組為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其頻率分布直方圖如圖所示.
,其頻率分布直方圖如圖所示.
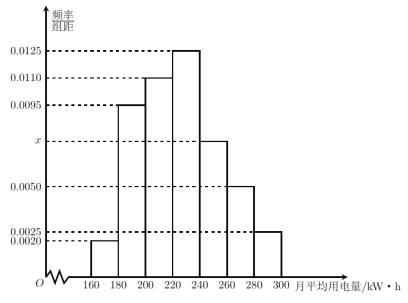
(1)若樣本中月均用電量在![]() 的居民有
的居民有![]() 戶,求樣本容量;
戶,求樣本容量;
(2)求月均用電量的中位數(shù);
(3)在月均用電量為![]() ,
,![]() ,
,![]() ,
,![]() 的四組居民中,用分層隨機(jī)抽樣法抽取
的四組居民中,用分層隨機(jī)抽樣法抽取![]() 戶居民,則月均用電量在
戶居民,則月均用電量在![]() 的居民應(yīng)抽取多少戶?
的居民應(yīng)抽取多少戶?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)某電子商務(wù)平臺的調(diào)查統(tǒng)計顯示,參與調(diào)查的1 000位上網(wǎng)購物者的年齡情況如圖所示.
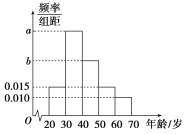
(1)已知[30,40),[40,50),[50,60)三個年齡段的上網(wǎng)購物者人數(shù)成等差數(shù)列,求![]() 的值;
的值;
(2)該電子商務(wù)平臺將年齡在[30,50)內(nèi)的人群定義為高消費人群,其他年齡段的人群定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發(fā)放代金券,高消費人群每人發(fā)放50元的代金券,潛在消費人群每人發(fā)放100元的代金券,現(xiàn)采用分層抽樣的方式從參與調(diào)查的1 000位上網(wǎng)購物者中抽取10人,并在這10人中隨機(jī)抽取3人進(jìn)行回訪,求此3人獲得代金券總和![]() (單位:元)的分布列與數(shù)學(xué)期望.
(單位:元)的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4,極坐標(biāo)與參數(shù)方程
已知在平面直角坐標(biāo)系![]() 中,
中,![]() 為坐標(biāo)原點,曲線
為坐標(biāo)原點,曲線![]() (
(![]() 為參數(shù)),在以平面直角坐標(biāo)系的原點為極點,
為參數(shù)),在以平面直角坐標(biāo)系的原點為極點,![]() 軸的正半軸為極軸,取相同單位長度的極坐標(biāo)系中,直線
軸的正半軸為極軸,取相同單位長度的極坐標(biāo)系中,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)直線![]() 與
與![]() 軸的交點
軸的交點![]() ,經(jīng)過點
,經(jīng)過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com