
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 過點(diǎn)
過點(diǎn)![]() ,傾斜角為
,傾斜角為![]() .以原點(diǎn)為極點(diǎn),
.以原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程
的極坐標(biāo)方程![]() .
.
(1)寫出直線![]() 的參數(shù)方程及曲線
的參數(shù)方程及曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() 為線段
為線段![]() 的中點(diǎn),且
的中點(diǎn),且![]() ,求
,求![]() .
.
【答案】(1)直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)), 曲線
為參數(shù)), 曲線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() .(2)
.(2)![]()
【解析】
(1)根據(jù)點(diǎn)![]() ,傾斜角為
,傾斜角為![]() 可得直線
可得直線![]() 的參數(shù)方程,兩邊同時(shí)乘以
的參數(shù)方程,兩邊同時(shí)乘以![]() 后,根據(jù)互化公式可得曲線
后,根據(jù)互化公式可得曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)將直線的參數(shù)方程代入拋物線方程,利用參數(shù)的幾何意義可解得結(jié)果.
(1)根據(jù)直線過點(diǎn)![]() ,傾斜角為
,傾斜角為![]() 可得直線
可得直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),
為參數(shù)),
由![]() 得
得![]() ,將
,將![]() ,
,![]() 代入可得
代入可得
曲線![]() 的直角坐標(biāo)方程:
的直角坐標(biāo)方程:![]() .
.
(2)將![]() ,
,![]() 代入到
代入到![]() ,得
,得![]() ,
,
設(shè)![]() 對應(yīng)的參數(shù)分別為
對應(yīng)的參數(shù)分別為![]() ,則
,則![]() 對應(yīng)的參數(shù)為
對應(yīng)的參數(shù)為![]() ,
,
由韋達(dá)定理得![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
由![]() ,所以
,所以![]() .
.


 同步學(xué)典一課多練系列答案
同步學(xué)典一課多練系列答案 經(jīng)典密卷系列答案
經(jīng)典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為4的菱形,∠BAD=60°,對角線AC與BD相交于點(diǎn)O,四邊形ACFE為梯形,EF//AC,點(diǎn)E在平面ABCD上的射影為OA的中點(diǎn),AE與平面ABCD所成角為45°.
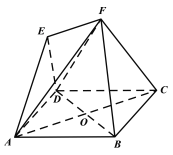
(Ⅰ)求證:BD⊥平面ACF;
(Ⅱ)求平面DEF與平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() .
.
(1)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的單調(diào)性和極小值(其中
的單調(diào)性和極小值(其中![]() 為自然對數(shù)的底數(shù));
為自然對數(shù)的底數(shù));
(2)若對任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱![]() 中,底面
中,底面![]() 為等邊三角形,E,F分別為
為等邊三角形,E,F分別為![]() ,
,![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() .
.
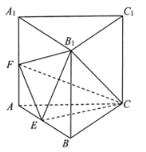
(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,有下述四個(gè)結(jié)論:
,有下述四個(gè)結(jié)論:
①若![]() 為
為![]() 的重心,則
的重心,則![]()
②若![]() 為
為![]() 邊上的一個(gè)動(dòng)點(diǎn),則
邊上的一個(gè)動(dòng)點(diǎn),則![]() 為定值2
為定值2
③若![]() ,
,![]() 為
為![]() 邊上的兩個(gè)動(dòng)點(diǎn),且
邊上的兩個(gè)動(dòng)點(diǎn),且![]() ,則
,則![]() 的最小值為
的最小值為![]()
④已知![]() 為
為![]() 內(nèi)一點(diǎn),若
內(nèi)一點(diǎn),若![]() ,且
,且![]() ,則
,則![]() 的最大值為2
的最大值為2
其中所有正確結(jié)論的編號(hào)是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
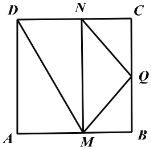
【題目】如圖,在邊長等于2正方形![]() 中,點(diǎn)Q是
中,點(diǎn)Q是![]() 中點(diǎn),點(diǎn)M,N分別在線段
中點(diǎn),點(diǎn)M,N分別在線段![]() 上移動(dòng)(M不與A,B重合,N不與C,D重合),且
上移動(dòng)(M不與A,B重合,N不與C,D重合),且![]() ,沿著
,沿著![]() 將四邊形
將四邊形![]() 折起,使得二面角
折起,使得二面角![]() 為直二面角,則三棱錐
為直二面角,則三棱錐![]() 體積的最大值為________;當(dāng)三棱錐
體積的最大值為________;當(dāng)三棱錐![]() 體積最大時(shí),其外接球的表面積為________.
體積最大時(shí),其外接球的表面積為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
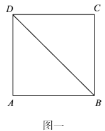
【題目】如圖一所示,四邊形![]() 是邊長為
是邊長為![]() 的正方形,沿
的正方形,沿![]() 將
將![]() 點(diǎn)翻折到
點(diǎn)翻折到![]() 點(diǎn)位置(如圖二所示),使得二面角
點(diǎn)位置(如圖二所示),使得二面角![]() 成直二面角.
成直二面角.![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).
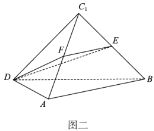
(1)求證:![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱錐![]() 中,面
中,面![]() 面
面![]() ,底面
,底面![]() 為矩形,且
為矩形,且![]() ,
,![]() ,
,![]() ,O為
,O為![]() 的中點(diǎn),點(diǎn)E在
的中點(diǎn),點(diǎn)E在![]() 上,且
上,且![]() .
.
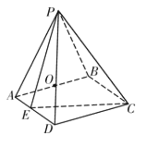
(1)證明:![]() ;
;
(2)在![]() 上是否存在一點(diǎn)F,使
上是否存在一點(diǎn)F,使![]() 面
面![]() ,若存在,試確定點(diǎn)F的位置.
,若存在,試確定點(diǎn)F的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】5人并排站成一行,如果甲乙兩人不相鄰,那么不同的排法種數(shù)是__________.(用數(shù)字作答);5人并排站成一行,甲乙兩人之間恰好有一人的概率是__________(用數(shù)字作答)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com