
如圖:四邊形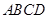 是梯形,
是梯形,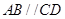 ,
,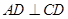 ,三角形
,三角形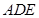 是等邊三角形,且平面
是等邊三角形,且平面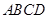
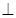 平面
平面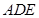 ,
,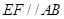 ,
,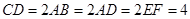 ,
,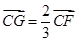
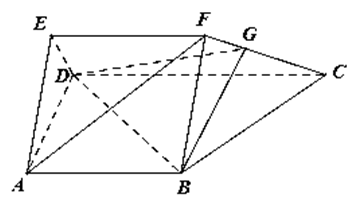
(1)求證: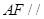 平面
平面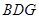 ;
;
(2)求二面角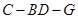 的余弦值.
的余弦值.
(1)詳見解析;(2)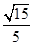
解析試題分析:(1)依據(jù)直線和平面平行的判定定理,要證明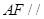 平面
平面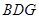 ,只需在平面
,只需在平面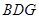 內(nèi)找一條直線與之平行,連接
內(nèi)找一條直線與之平行,連接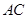 交
交 于
于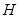 ,連接
,連接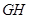 ,易證
,易證 ,故
,故 ,進(jìn)而證明
,進(jìn)而證明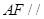 平面
平面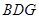 (2)以
(2)以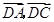 所在的直線,過點(diǎn)
所在的直線,過點(diǎn)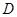 垂直于面
垂直于面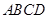 的直線分別為
的直線分別為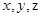 軸,建立空間直角坐標(biāo)系,求相關(guān)點(diǎn)的坐標(biāo),再求半平面
軸,建立空間直角坐標(biāo)系,求相關(guān)點(diǎn)的坐標(biāo),再求半平面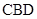 和
和 的法向量,再求兩個法向量的夾角的余弦值,進(jìn)而可得二面角
的法向量,再求兩個法向量的夾角的余弦值,進(jìn)而可得二面角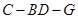 的余弦值.
的余弦值.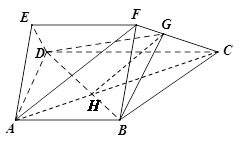
試題解析:解:(1)連接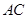 交
交 于
于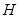 ,連接
,連接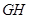 .
.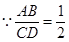 ,
, 即
即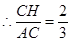
 ,
,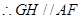 ,
, 平面
平面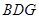 ,
,

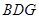 ,
, 平面
平面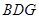 .
.
(2) 如圖建立空間坐標(biāo)系,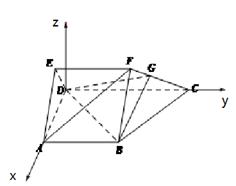
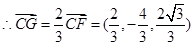
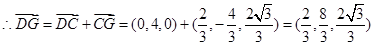
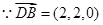 ,設(shè)平面
,設(shè)平面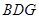 的法向量為
的法向量為 ,
,
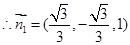 -
-
設(shè)平面 的法向量為
的法向量為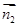 ,
,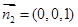
 ,所以二面角
,所以二面角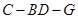 的余弦值為
的余弦值為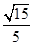 .
.
考點(diǎn):1、直線和平面平行的判定;2、二面角.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,五面體中,四邊形ABCD是矩形,DA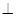 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,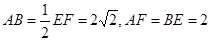 ,P、Q、M分別為AE、BD、EF的中點(diǎn).
,P、Q、M分別為AE、BD、EF的中點(diǎn).
求證:(I)PQ//平面BCE;
(II)求證:AM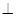 平面ADF;
平面ADF;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖1,在直角梯形 中,
中,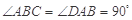 ,
, ,
,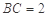 ,
,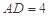 . 把
. 把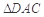 沿對角線
沿對角線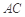 折起到
折起到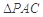 的位置,如圖2所示,使得點(diǎn)
的位置,如圖2所示,使得點(diǎn)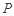 在平面
在平面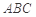 上的正投影
上的正投影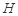 恰好落在線段
恰好落在線段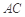 上,連接
上,連接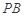 ,點(diǎn)
,點(diǎn)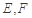 分別為線段
分別為線段 的中點(diǎn).
的中點(diǎn). 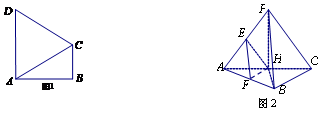
(1)求證:平面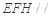 平面
平面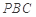 ;
;
(2)求直線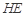 與平面
與平面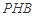 所成角的正弦值;
所成角的正弦值;
(3)在棱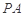 上是否存在一點(diǎn)
上是否存在一點(diǎn) ,使得
,使得 到點(diǎn)
到點(diǎn)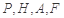 四點(diǎn)的距離相等?請說明理由.
四點(diǎn)的距離相等?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
正方體 的棱長為
的棱長為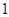 ,線段
,線段 上有兩個動點(diǎn)
上有兩個動點(diǎn) ,且
,且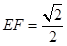 ,則下列結(jié)論中錯誤的是( )
,則下列結(jié)論中錯誤的是( )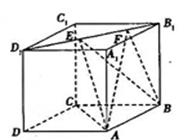
A.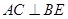 |
B.三棱錐 的體積為定值 的體積為定值 |
C.二面角 的大小為定值 的大小為定值 |
D.異面直線 所成角為定值 所成角為定值 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,兩座建筑物AB,CD的底部都在同一個水平面上,且均與水平面垂直,它們的高度分別是9m和15m,從建筑物AB的頂部A看建筑物CD的張角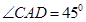 .
.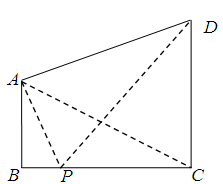
(1)求BC的長度;
(2)在線段BC上取一點(diǎn)P(點(diǎn)P與點(diǎn)B,C不重合),從點(diǎn)P看這兩座建筑物的張角分別為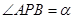 ,
, ,問點(diǎn)P在何處時,
,問點(diǎn)P在何處時,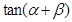 最小?
最小?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
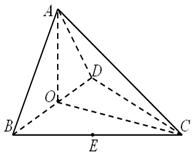
如圖,四面體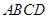 中,
中,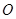 、
、 分別是
分別是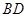 、
、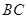 的中點(diǎn),
的中點(diǎn),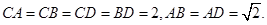
(Ⅰ)求證: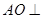 平面
平面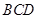 ;
;
(Ⅱ)求二面角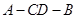 的正切值;
的正切值;
(Ⅲ)求點(diǎn) 到平面
到平面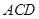 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.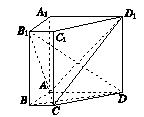
(1)證明:AC⊥B1D;
(2)求直線B1C1與平面ACD1所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,PDCE為矩形,ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=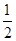 CD=1,PD=
CD=1,PD= 。
。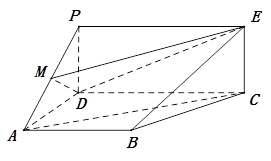
(I)若M為PA中點(diǎn),求證:AC∥平面MDE;
(II)求直線PA與平面PBC所成角的正弦值;
(III)在線段PC上是否存在一點(diǎn)Q(除去端點(diǎn)),使得平面QAD與平面PBC所成銳二面角的大小為 ?
?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com