【題目】設過拋物線
的焦點
的直線
交拋物線于點
，若以
為直徑的圓過點
，且與
軸交于
， 
兩點，則
（ ）
A. 3 B. 2 C. -3 D. -2
【答案】C
【解析】拋物線焦點坐標為F（1，0），準線方程為x=﹣1
設直線MN的方程為x=ty+1，A、B的坐標分別為（
，y1），（
，y2）
聯立直線和拋物線得到方程：y2﹣4my﹣4=0，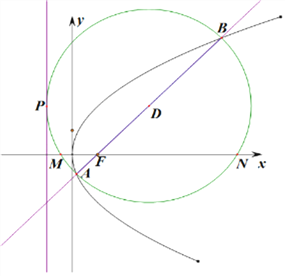
∴y1+y2=4m，y1y2=﹣4，
x1+x2=ty1+1+ty2+1=t（y1+y2）+2=4t2+2， 
=2t2+1， 
=2t，
則圓心D（2t2+1，2t），
由拋物線的性質可知：丨AB丨=x1+x2+p=4（t2+1），
由P到圓心的距離d=
，由題意可知：d=
丨AB丨，
解得：t=1，則圓心為（3，2），半徑為4，∴圓的方程方程為（x﹣3）2+（y﹣2）2=42，
則當y=0，求得與x軸的交點坐標，假設m＞n，則m=3﹣2
，n=3+2
，
∴mn=（3﹣2
）（3+2
）=﹣3，
故選：C．
培優三好生系列答案
優化作業上海科技文獻出版社系列答案科目：高中數學 來源： 題型：
【題目】三棱錐P﹣ABC中，底面△ABC滿足BA=BC， 
，P在面ABC的射影為AC的中點，且該三棱錐的體積為 
，當其外接球的表面積最小時，P到面ABC的距離為（ ）
A.2
B.3
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年3月14日，“
共享單車”終于來到蕪湖，共享單車又被親切稱作“小黃車”是全球第一個無樁共享單車平臺，開創了首個“單車共享”模式．相關部門準備對該項目進行考核，考核的硬性指標是：市民對該項目的滿意指數不低于
，否則該項目需進行整改，該部門為了了解市民對該項目的滿意程度，隨機訪問了使用共享單車的
名市民，并根據這名市民對該項目滿意程度的評分（滿分分），繪制了如下頻率分布直方圖：
（I）為了了解部分市民對“共享單車”評分較低的原因，該部門從評分低于
分的市民中隨機抽取
人進行座談，求這人評分恰好都在
的概率；
（II）根據你所學的統計知識，判斷該項目能否通過考核，并說明理由．
（注：滿意指數=
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】棉花的纖維長度是評價棉花質量的重要指標，某農科所的專家在土壤環境不同的甲、乙兩塊實驗地分別種植某品種的棉花，為了評價該品種的棉花質量，在棉花成熟后，分別從甲、乙兩地的棉花中各隨機抽取20根棉花纖維進行統計，結果如下表：（記纖維長度不低于300mm的為“長纖維”，其余為“短纖維”）
纖維長度 | （0，100） | [100，200） | [200，300） | [300，400） | [400，500] |
甲地（根數） | 3 | 4 | 4 | 5 | 4 |
乙地（根數） | 1 | 1 | 2 | 10 | 6 |
（1）由以上統計數據，填寫下面2×2列聯表，并判斷能否在犯錯誤概率不超過0.025的前提下認為“纖維長度與土壤環境有關系”．
甲地 | 乙地 | 總計 | |
長纖維 | |||
短纖維 | |||
總計 |
附：（1） 
；（2）臨界值表；
P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（2）現從上述40根纖維中，按纖維長度是否為“長纖維”還是“短纖維”采用分層抽樣的方法抽取8根進行檢測，在這8根纖維中，記乙地“短纖維”的根數為X，求X的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市醫療保險實行定點醫療制度，按照“就近就醫、方便管理” 的原則，規定參加保險人員可自主選擇四家醫療保險定點醫院和一家社區醫院作為就診的醫療機構.若甲、乙、丙、丁4名參加保險人員所在地區附近有
三家社區醫院，并且他們的選擇是等可能的、相互獨立的.
（1）求甲、乙兩人都選擇
社區醫院的概率；
（2）求甲、乙兩人不選擇同一家社區醫院的概率；
（3）設在4名參加保險人員中選擇
社區醫院的人數為
，求
的分布列和數學期望及方差.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2＋(y－1)2＝5，直線l：mx－y＋1－m＝0(m∈R)．
(1)判斷直線l與圓C的位置關系；
(2)設直線l與圓C交于A，B兩點，若直線l的傾斜角為120°，求弦AB的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD的底面ABCD是平行四邊形，側面PAD是邊長為2的正三角形，AB=BD= 
，PB= 
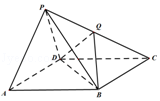
（Ⅰ）求證：平面PAD⊥平面ABCD；
（Ⅱ）設Q是棱PC上的點，當PA∥平面BDQ時，求二面角A﹣BD﹣Q的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在直角梯形
中，
，
，且
．現以
為一邊向形外作正方形
，然后沿邊將正方形翻折，使平面與平面垂直，
為
的中點，如圖2．
（1）求證：
平面
；
（2）求證：
平面
；
（3）求三棱錐
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com