(本題14分)已知數列

中,

(1)求證:數列

與

都是等比數列;
(2) 若數列

前

的和為

,令

,求數列

的最大項.
(1)∵

,∴

∴數列

是以1為首項,

為公比的等比數列;
數列

是以

為首項,

為公比的等比數列。
(2)







∴

練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
已知數列

滿足:

,其中

為數列

的前

項和.
(1)試求數列

的通項公式;
(2)設

,數列

的前

項和為

,求證

查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
) (本題滿分14分) 設等差數列{
an}的首項
a1為
a,前
n項和為
Sn.
(Ⅰ) 若
S1,
S2,
S4成等比數列,求數列{
an}的通項公式;
(Ⅱ) 證明:
 n
n∈N*,
Sn,
Sn+1,
Sn+2不構成等比數列.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本題滿分14分)在數列

中,

為其前

項和,滿足

.(I)若

,求數列

的通項公式;
(II)若數列

為公比不為1的等比數列,求

.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列

的相鄰兩項

是關于

的方程

的兩根,且

(1)求證:數列

是等比數列;
(2)求數列

的前

項和

;
(3)若

對任意的

都成立,求

的取值范圍。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分14分)
數列
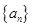
滿足
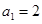
,
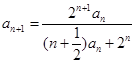
(
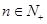
).
(1)設
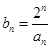
,求數列
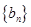
的通項公式
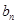
;
(2)設
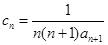
,數列
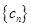
的前
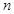
項和為
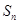
,求
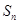
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)已知數列
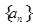
的前
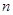
項和為
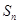
,且
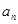
是
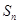
與2的等差中項,數列
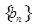
中,
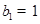
,點
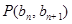
在直線
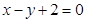
上.
⑴求
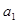
和
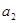
的值;
⑵求數列
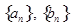
的通項
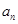
和
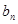
;
⑶ 設
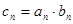
,求數列
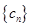
的前n項和
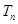
.
查看答案和解析>>
主站蜘蛛池模板:
一区二区三区四区免费观看
|
久久久久久久久久久高潮
|
日本黄色三级网站
|
国产一级大片
|
亚洲一区二区在线免费观看
|
一区二区在线看
|
久久视频在线
|
国产精品片aa在线观看
|
男人天堂手机在线视频
|
亚洲国产成人在线
|
亚洲va欧美va人人爽成人影院
|
国产美女在线免费
|
欧美在线一区二区三区
|
波多野结衣一区二区三区高清
|
欧洲精品|
国产一区二区精品在线
|
色吊丝2288sds中文字幕
|
日韩三区
|
国产在线一级片
|
国产成人免费视频
|
夜夜春精品视频高清69式
|
亚洲jizzjizz日本少妇
|
欧美一区二区三区四区不卡
|
欧美激情精品久久久久久
|
av网站观看
|
国产伦理精品一区二区三区观看体验
|
欧美日韩不卡在线
|
亚洲成人免费影院
|
九九热精品在线
|
美女视频黄的免费
|
蜜桃视频麻豆女神沈芯语免费观看
|
国产一级片在线播放
|
男女免费视频
|
国产偷录视频叫床高潮对白
|
亚洲午夜精品一区二区三区他趣
|
欧美三级视频
|
日韩欧美在线视频播放
|
久久综合狠狠综合久久综合88
|
国产精品视频久久久
|
日本在线一区二区
|
亚洲精品国产精品乱码不99按摩
|

 中,
中,
 與
與 都是等比數列;
都是等比數列; 前
前 的和為
的和為 ,令
,令 ,求數列
,求數列 的最大項.
的最大項. n∈N*, Sn,Sn+1,Sn+2不構成等比數列.
n∈N*, Sn,Sn+1,Sn+2不構成等比數列.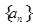 的前
的前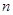 項和為
項和為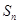 ,且
,且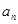 是
是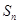 與2的等差中項,數列
與2的等差中項,數列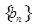 中,
中,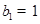 ,點
,點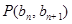 在直線
在直線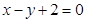 上.
上.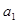 和
和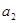 的值;
的值;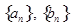 的通項
的通項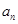 和
和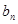 ;
;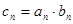 ,求數列
,求數列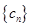 的前n項和
的前n項和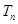 .
.