
��֪ �Dz�ȫ��
�Dz�ȫ�� �Č�(sh��)��(sh��)������(sh��)
��(sh��)��(sh��)������(sh��) ��
�� ������
������ �Ќ�(sh��)������
�Ќ�(sh��)������ �Č�(sh��)��(sh��)������
�Č�(sh��)��(sh��)������ �ĸ�����֮��
�ĸ�����֮�� �Č�(sh��)��(sh��)������
�Č�(sh��)��(sh��)������ �ĸ���
�ĸ���
��1���� ��ֵ����2����
��ֵ����2���� ����
���� ��ȡֵ������
��ȡֵ������
��1��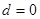 ����2��
����2��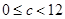 .
.
����ԇ�}��������1����С�}�Ќ�(du��)��֪�l����������һ��(g��)�P(gu��n)�I�c(di��n)�����O(sh��)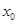 ��
��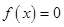 �ĸ��������
�ĸ��������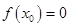 ����
����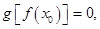 �t��
�t��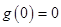 ���Ķ���(du��)�ں���(sh��)
���Ķ���(du��)�ں���(sh��) ���ԣ��ɵ�
���ԣ��ɵ�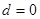 .
.
��2����С�}����?y��n)��?img src="http://thumb.zyjl.cn/pic5/tikupic/80/7/1wkg34.png" style="vertical-align:middle;" />������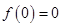 ���ֿ�֪
���ֿ�֪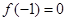 ������
������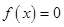 �ĸ���0��-1����(du��)�ڌ�(sh��)��(sh��)
�ĸ���0��-1����(du��)�ڌ�(sh��)��(sh��) ���·֞�����(sh��)��ؓ(f��)��(sh��)�c�����N��r�M(j��n)��ӑՓ.
���·֞�����(sh��)��ؓ(f��)��(sh��)�c�����N��r�M(j��n)��ӑՓ.
ԇ�}��������1���O(sh��)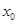 ��
��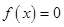 �ĸ�����ô
�ĸ�����ô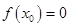 ���t
���t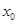 ��
�� �ĸ����t
�ĸ����t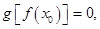 ��
��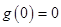 ������
������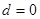 ��
��
��2�� ������
������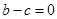 ����
����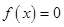 �ĸ���0��-1��
�ĸ���0��-1��
�ٮ�(d��ng)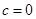 �r(sh��)���t
�r(sh��)���t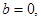 �@�r(sh��)
�@�r(sh��)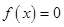 �ĸ���һ�Ќ�(sh��)��(sh��)����
�ĸ���һ�Ќ�(sh��)��(sh��)����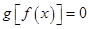 ������
������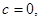 ����Ҫ��
����Ҫ��
��(d��ng)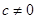 �r(sh��)����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/c3/5/9sgth2.png" style="vertical-align:middle;" />=0�ĸ������ܞ�0��
�r(sh��)����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/c3/5/9sgth2.png" style="vertical-align:middle;" />=0�ĸ������ܞ�0��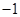 ������
������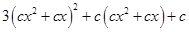 ��?z��)o��(sh��)��(sh��)����
��?z��)o��(sh��)��(sh��)����
�ڮ�(d��ng)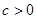 �r(sh��)��
�r(sh��)��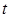 =
=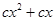 =
=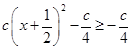 ��������(sh��)
��������(sh��)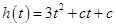 ��
��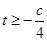 ��
��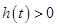 ���������
���������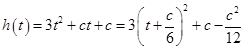 ������
������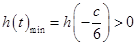 ����
����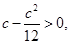 ����
����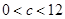 ���ۮ�(d��ng)
���ۮ�(d��ng)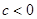 �r(sh��)��
�r(sh��)��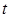 =
=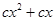 =
=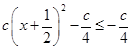 ��������(sh��)
��������(sh��)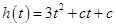 ��
��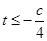 ��
��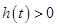 ���������
���������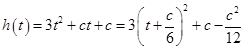 ������
������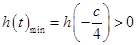 ��
��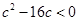 ����
����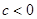 ����ȥ���C������������
����ȥ���C������������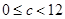 .
.
���c(di��n)������(sh��)�����c(di��n)������̵ĸ�������(f��)�Ϻ���(sh��)�������(sh��)ֵ��(w��n)�}���䷽�������(l��i)ӑՓ˼��.


 ���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д�
���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д� ���o(j��)��ͨ��(y��u)���y(c��)ϵ�д�
���o(j��)��ͨ��(y��u)���y(c��)ϵ�д� �ٷW(xu��)�����I(y��)���}����ϵ�д�
�ٷW(xu��)�����I(y��)���}����ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����(sh��)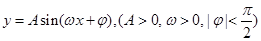 ����Сֵ��
����Сֵ�� ����һ��(g��)���ڃ�(n��i)�D������c(di��n)�c����c(di��n)�M����(bi��o)����
����һ��(g��)���ڃ�(n��i)�D������c(di��n)�c����c(di��n)�M����(bi��o)����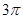 ���֣��D���^(gu��)�c(di��n)
���֣��D���^(gu��)�c(di��n)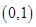 ��
��
��1������(sh��)����ʽ��
��2������(sh��)�����ֵ���Լ��_(d��)�����ֵ�r(sh��) �ļ��ϣ�
�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) ����(d��ng)
����(d��ng) �r(sh��)������
�r(sh��)������ ��
��
(1)���C�� ���溯��(sh��)��
���溯��(sh��)��
(2)��� ������(sh��)��(sh��)��
������(sh��)��(sh��)�� ������
������ ��ԇ��
��ԇ�� �څ^(q��)�g[��2,6]�ϵ���ֵ��
�څ^(q��)�g[��2,6]�ϵ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪ �Ƕ��x��
�Ƕ��x�� �ϵ��溯��(sh��)����
�ϵ��溯��(sh��)���� ����
���� �r(sh��)����
�r(sh��)����
��1���C�� ��
�� ����������(sh��)��
����������(sh��)��
��2���ⲻ��ʽ
��3���� ��(du��)
��(du��) ���������(sh��)��(sh��)
���������(sh��)��(sh��) ��ȡֵ����
��ȡֵ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪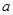 �錍(sh��)��(sh��)��
�錍(sh��)��(sh��)��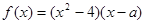 ��
��
��1����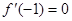 ����
���� ��
��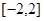 �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2���� ��
��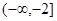 ��
��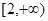 �϶����f���ģ���
�϶����f���ģ���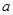 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪
��1���Д� ����ż�ԣ�
����ż�ԣ�
��2��ӑՓ �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��3����(d��ng) �r(sh��)��
�r(sh��)�� ���������b��ȡֵ����.
���������b��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)f(x)��2x��x��R.��(d��ng)mȡ��ֵ�r(sh��)����|f(x)��2|��m��һ��(g��)�⣿?j��)ɂ�(g��)�⣿
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com