
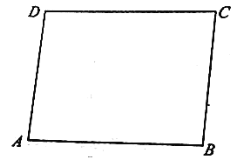
【題目】如圖,矩形![]() 是某生態農莊的一塊植物栽培基地的平面圖,現欲修一條筆直的小路
是某生態農莊的一塊植物栽培基地的平面圖,現欲修一條筆直的小路![]() (寬度不計)經過該矩形區域,其中
(寬度不計)經過該矩形區域,其中![]() 都在矩形
都在矩形![]() 的邊界上.已知
的邊界上.已知![]() ,
,![]() (單位:百米),小路
(單位:百米),小路![]() 將矩形
將矩形![]() 分成面積分別為
分成面積分別為![]() ,
,![]() (單位:平方百米)的兩部分,其中
(單位:平方百米)的兩部分,其中![]() ,且點
,且點![]() 在面積為
在面積為![]() 的區域內,記小路
的區域內,記小路![]() 的長為
的長為![]() 百米.
百米.
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】某單位對員工業務進行考核,從![]() 類員工(工作3年及3年以內的員工)和
類員工(工作3年及3年以內的員工)和![]() 類員工(工作3年以上的員工)的成績中各抽取15個,具體數據如下:
類員工(工作3年以上的員工)的成績中各抽取15個,具體數據如下:

![]() 類成績:20 10 22 30 15 12 41 22 31 25 12 26 29 32 33
類成績:20 10 22 30 15 12 41 22 31 25 12 26 29 32 33
![]() 類成績:21 40 30 41 42 31 49 51 52 43 47 47 32 45 48
類成績:21 40 30 41 42 31 49 51 52 43 47 47 32 45 48
(1)根據兩組數據完成兩類員工成績的莖葉圖,并通過莖葉圖比較兩類員工成績的平均值及分散程度(不要求計算出具體值,得出結論即可);
(2)研究發現從業時間與業務能力之間具有線性相關關系,從上述抽取的![]() 名員工中抽取4名員工的成績如下:
名員工中抽取4名員工的成績如下:
員工工作時間 | 1 | 2 | 3 | 4 |
考核成績 | 10 | 15 | 20 | 30 |
根據四個的數據,求![]() 關于
關于![]() 的線性回歸方程.
的線性回歸方程.
附:回歸直線![]() 的斜率和截距的最小二乘法估計公式分別為:
的斜率和截距的最小二乘法估計公式分別為: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國大學先修課程,是在高中開設的具有大學水平的課程,旨在讓學有余力的高中生早接受大學思維方式、學習方法的訓練,為大學學習乃至未來的職業生涯做好準備.某高中開設大學先修課程已有兩年,兩年共招收學生2000人,其中有300人參與學習先修課程,兩年全校共有優等生200人,學習先修課程的優等生有60人.這兩年學習先修課程的學生都參加了考試,并且都參加了某高校的自主招生考試(滿分100分),結果如下表所示:
分數 |
|
|
|
|
|
人數 | 20 | 55 | 105 | 70 | 50 |
參加自主招生獲得通過的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填寫列聯表,并畫出列聯表的等高條形圖,并通過圖形判斷學習先修課程與優等生是否有關系,根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過0.01的前提下認為學習先修課程與優等生有關系?

優等生 | 非優等生 | 總計 | |
學習大學先修課程 | |||
沒有學習大學先修課程 | |||
總計 |
(2)已知今年有150名學生報名學習大學先修課程,以前兩年參加大學先修課程學習成績的頻率作為今年參加大學先修課程學習成績的概率.
①在今年參與大學先修課程的學生中任取一人,求他獲得某高校自主招生通過的概率;
②設今年全校參加大學先修課程的學生獲得某高校自主招生通過的人數為![]() ,求
,求![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個結論:
①若![]() 在
在![]() 上是奇函數,則
上是奇函數,則![]() 在
在![]() 上也是奇函數
上也是奇函數
②若![]() 不是正弦函數,則
不是正弦函數,則![]() 不是周期函數
不是周期函數
③“若![]() ,則
,則![]() .”的否命題是“若
.”的否命題是“若![]() ,則
,則![]() .”
.”
④若![]() :
:![]() ;
;![]() :
:![]() ,則
,則![]() 是
是![]() 的充分不必要條件
的充分不必要條件
其中正確結論的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別為雙曲線
分別為雙曲線![]()
![]()
![]() 的左、右焦點,點P是以
的左、右焦點,點P是以![]() 為直徑的圓與C在第一象限內的交點,若線段
為直徑的圓與C在第一象限內的交點,若線段![]() 的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
的中點Q在C的漸近線上,則C的兩條漸近線方程為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
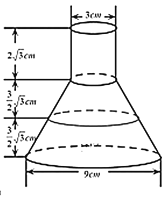
【題目】《烏鴉喝水》是《伊索寓言》中一個寓言故事,通過講述已知烏鴉喝水的故事,告訴人們遇到困難要運用智慧,認真思考才能讓問題迎刃而解的道理,如圖![]() 所示,烏鴉想喝水,發現有一個錐形瓶,上面部分是圓柱體,下面部分是圓臺,瓶口直徑為
所示,烏鴉想喝水,發現有一個錐形瓶,上面部分是圓柱體,下面部分是圓臺,瓶口直徑為![]() 厘米,瓶底直徑為
厘米,瓶底直徑為![]() 厘米,瓶口距瓶頸為
厘米,瓶口距瓶頸為![]() 厘米,瓶頸到水位線距離和水位線到瓶底距離均為
厘米,瓶頸到水位線距離和水位線到瓶底距離均為![]() 厘米,現將
厘米,現將![]() 顆石子投入瓶中,發現水位線上移
顆石子投入瓶中,發現水位線上移![]() 厘米,若只有當水位線到達瓶口時烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是( )
厘米,若只有當水位線到達瓶口時烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是( )
A.![]() 顆B.
顆B.![]() 顆C.
顆C.![]() 顆D.
顆D.![]() 顆
顆
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)設各項均為正數的等比數列![]() 中,
中,![]()
![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,求證:
,求證: ![]() ;
;
(3)是否存在正整數![]() ,使得
,使得![]() 對任意正整數
對任意正整數![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值,若不存在,說明理由.
的最大值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面上到兩個定點的距離的積為定值的動點軌跡一般稱為卡西尼(cassin)卵形線,已知曲線![]() 為到定點
為到定點![]() 的距離之積為常數4的點
的距離之積為常數4的點![]() 的軌跡,關于曲線
的軌跡,關于曲線![]() 的幾何性質有下四個結論,其中錯誤的是( )
的幾何性質有下四個結論,其中錯誤的是( )
A.曲線![]() 關于原點對稱B.
關于原點對稱B.![]() 的面積的最大值為2
的面積的最大值為2
C.其中![]() 的取值范圍為
的取值范圍為![]() D.其中
D.其中![]() 的取值范圍為
的取值范圍為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在橢圓![]() 上任取一點
上任取一點![]() (
(![]() 不為長軸端點),連結
不為長軸端點),連結![]() 、
、![]() ,并延長與橢圓
,并延長與橢圓![]() 分別交于點
分別交于點![]() 、
、![]() 兩點,已知
兩點,已知![]() 的周長為8,
的周長為8,![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設坐標原點為![]() ,當
,當![]() 不是橢圓的頂點時,直線
不是橢圓的頂點時,直線![]() 和直線
和直線![]() 的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com