
分析 根據余弦定理和正弦定理將條件進行化簡,結合向量數量積的定義進行求解即可.
解答 解:在△ABC中,∵a2+b2-c2=$\sqrt{3}$ab,
∴由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{\sqrt{3}ab}{2ab}=\frac{\sqrt{3}}{2}$,
則C=$\frac{π}{6}$,
∵acsinB=2$\sqrt{3}$sinC,
∴由正弦定理得ac•b=2$\sqrt{3}$c,
即ab=2$\sqrt{3}$,
則$\overrightarrow{CA}$•$\overrightarrow{CB}$=|$\overrightarrow{CA}$|•|$\overrightarrow{CB}$|cosC=abcosC=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
故答案為:3.
點評 本題主要考查向量數量積的求解,根據正弦定理和余弦定理進行化簡是解決本題的關鍵.考查學生的轉化能力.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:高中數學 來源: 題型:解答題
 某工廠隨機抽取部分工人調查其上班路上所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),若上班路上所需時間的范圍是[0,100],樣本數據分組為[0,20),[20,40),[40,60),[60,80),[80,100].
某工廠隨機抽取部分工人調查其上班路上所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),若上班路上所需時間的范圍是[0,100],樣本數據分組為[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中數學 來源: 題型:解答題
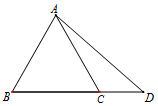 如圖,△ABC是等邊三角形,點D在邊BC的延長線上,且BC=2CD,AD=$\sqrt{7}$.
如圖,△ABC是等邊三角形,點D在邊BC的延長線上,且BC=2CD,AD=$\sqrt{7}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{4}$ | C. | 0 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{1}{2},+∞)$ | B. | $[\frac{1}{2},+∞)$ | C. | $(\frac{1}{4},+∞)$ | D. | $[\frac{1}{4},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com