
【題目】(本小題滿分12分)
在如圖所示的多面體中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.

(1)求證:![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1) 解法1

證明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . …………2分
. …………2分
過![]() 作
作![]() 交
交![]() 于
于![]() ,則
,則![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() . …………4分
. …………4分
∵![]() ,∴四邊形
,∴四邊形![]() 平行四邊形,
平行四邊形,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴四邊形![]() 為正方形,
為正方形,
∴![]() , ……………6分
, ……………6分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() . ………………………7分
. ………………………7分
∵![]() 平面
平面![]() ,
,
∴![]() . ………………………8分
. ………………………8分
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]()
由(1)可知![]()
∴![]() ⊥平面
⊥平面![]()
∵![]() 平面
平面![]()
∴![]() ……………………9分
……………………9分
取![]() 的中點
的中點![]() ,連結(jié)
,連結(jié)![]() ,
,![]()
∵四邊形![]() 是正方形,
是正方形,
∴![]()
∵![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ⊥平面
⊥平面![]()
∴![]() ⊥
⊥![]() Z|X|X|K]
Z|X|X|K]
∴![]() 是二面角
是二面角![]() 的平面角, ………………………12分
的平面角, ………………………12分
由計算得![]()
∴![]() ………………………13分
………………………13分
∴平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .………………………14分
.………………………14分
解法2
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,
,
∴![]() 兩兩垂直. ……………………2分
兩兩垂直. ……………………2分
以點E為坐標原點,![]() 分別為
分別為![]() 軸建立如圖所示的空間直角坐標系.
軸建立如圖所示的空間直角坐標系.

由已知得,![]() (0,0,2),
(0,0,2),![]() (2,0,0),
(2,0,0),
![]() (2,4,0),
(2,4,0),![]() (0,3,0),
(0,3,0),![]() (0,2,2),
(0,2,2),
![]() (2,2,0). …………………………4分
(2,2,0). …………………………4分
∴![]() ,
,![]() ,………6分
,………6分
∴![]() , ………7分
, ………7分
∴![]() . …………………………8分
. …………………………8分
(2)由已知得![]() 是平面
是平面![]() 的法向量. ………………………9分
的法向量. ………………………9分
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
∵![]() ,
,
∴ ,即
,即![]() ,令
,令![]() ,得
,得![]() . ……………12分
. ……………12分
設(shè)平面![]() 與平面
與平面![]() 所成銳二面角的大小為
所成銳二面角的大小為![]() ,
,
則![]() …………………………13分
…………………………13分
∴平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() . …………………………14分
. …………………………14分
【解析】
(1)證明EB,EF,EA兩兩垂直,以點E為坐標原點,EB,EF,EA分別為x,y,z軸,建立空間直角坐標系用坐標表示點與向量,證明
![]() ,可得BD⊥EG;
,可得BD⊥EG;
(2)由已知得![]() 是平面DEF的法向量,求出平面DEG的法向量
是平面DEF的法向量,求出平面DEG的法向量
![]() ,利用向量的夾角公式,可求平面DEG與平面DEF所成銳二面角的余弦值.
,利用向量的夾角公式,可求平面DEG與平面DEF所成銳二面角的余弦值.
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .又
.又![]() ,
,
![]() BE,EF,AE兩兩垂直.
BE,EF,AE兩兩垂直.
以點E為坐標原點,EB,EF,EA分別為x,y,z軸,
建立空間直角坐標系,
由已知得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
(Ⅱ)由已知得![]() 是平面DEF的法向量,
是平面DEF的法向量,
設(shè)平面的DEG法向量為![]() ,
,
![]() ,
,![]() ,
,
 即
即![]() 令
令![]() ,得
,得![]() ,
,
設(shè)平面DEG與平面DEF所成銳二面角的大小為θ,
則 .
.
![]() 平面DEG與平面DEF所成銳二面角的余弦值為
平面DEG與平面DEF所成銳二面角的余弦值為![]() .
.


 手拉手全優(yōu)練考卷系列答案
手拉手全優(yōu)練考卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 對任意
對任意![]() 、
、![]() 都有
都有![]() ,且當
,且當![]() 時,
時,![]() .
.
(1)證明![]() 為奇函數(shù);
為奇函數(shù);
(2)證明![]() 在R上是減函數(shù);
在R上是減函數(shù);
(3)若![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小李從網(wǎng)上購買了一件商品,快遞員計劃在下午5:00-6:00之間送貨上門,已知小李下班到家的時間為下午5:30-6:00.快遞員到小李家時,如果小李未到家,則快遞員會電話聯(lián)系小李.若小李能在10分鐘之內(nèi)到家,則快遞員等小李回來;否則,就將商品存放在快遞柜中.則小李需要去快遞柜收取商品的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“互聯(lián)網(wǎng)![]() ”是“智慧城市”的重要內(nèi)士,
”是“智慧城市”的重要內(nèi)士,![]() 市在智慧城市的建設(shè)中,為方便市民使用互聯(lián)網(wǎng),在主城區(qū)覆蓋了免費
市在智慧城市的建設(shè)中,為方便市民使用互聯(lián)網(wǎng),在主城區(qū)覆蓋了免費![]() .為了解免費
.為了解免費![]() 在
在![]() 市的使用情況,調(diào)査機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)査的網(wǎng)友中抽取了
市的使用情況,調(diào)査機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)査的網(wǎng)友中抽取了![]() 人進行抽樣分析,得到如下列聯(lián)表(單位:人):
人進行抽樣分析,得到如下列聯(lián)表(單位:人):
經(jīng)常使用免費WiFi | 偶爾或不用免費WiFi | 合計 | |
45歲及以下 | 70 | 30 | 100 |
45歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據(jù)以上數(shù)據(jù),判斷是否有![]() 的把握認為
的把握認為![]() 市使用免費
市使用免費![]() 的情況與年齡有關(guān);
的情況與年齡有關(guān);
(2)將頻率視為概率,現(xiàn)從該市![]() 歲以上的市民中用隨機抽樣的方法每次抽取
歲以上的市民中用隨機抽樣的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.記被抽取的
次.記被抽取的![]() 人中“偶爾或不用免費
人中“偶爾或不用免費![]() ”的人數(shù)為
”的人數(shù)為![]() ,若每次抽取的結(jié)果是相互獨立的,求
,若每次抽取的結(jié)果是相互獨立的,求![]() 的分布列,數(shù)學期望
的分布列,數(shù)學期望![]() 和方差
和方差![]() .
.
附: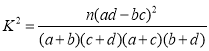 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義在R上的偶函數(shù)f(x),其導函數(shù)![]() ,當x≥0時,恒有
,當x≥0時,恒有![]()
![]() +f(﹣x)<0,若g(x)=x2f(x),則不等式g(x)<g(1﹣2x)的解集為( )
+f(﹣x)<0,若g(x)=x2f(x),則不等式g(x)<g(1﹣2x)的解集為( )
A.(![]() ,1)B.(﹣∞,
,1)B.(﹣∞,![]() )∪(1,+∞)
)∪(1,+∞)
C.(![]() ,+∞)D.(﹣∞,
,+∞)D.(﹣∞,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ),其中
),其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)已知![]() ,
, ![]() 為整數(shù),若對任意
為整數(shù),若對任意![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校大一新生中的6名同學打算參加學校組織的“演講團”、“吉他協(xié)會”等五個社團,若每名同學必須參加且只能參加1個社團且每個社團至多兩人參加,則這6個人中沒有人參加“演講團”的不同參加方法數(shù)為( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,直線![]() 經(jīng)過點
經(jīng)過點![]() ,傾斜角
,傾斜角![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() .
.
(Ⅰ)求曲線C的直角坐標方程并寫出直線l的參數(shù)方程;
(Ⅱ)直線l與曲線C的交點為A,B,求點P到A、B兩點的距離之積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com