Question

函數y=3|sinx|+sinx-k在[0，2π]上有且僅有兩個零點，則k的取值范圍是    ．

Answer 1

【答案】分析：根據題意可得：當x∈[0，π]時，sinx≥0，函數g（x）=4sinx≥0；當x∈[π，2π]時，sinx≤0，函數g（x）=-2sinx≥0，即可結合正弦函數的性質畫出函數的圖象，進而根據數形結合與轉化化歸的思想方法把函數零點問題轉化為兩個函數的交點問題，即可求出k的取值范圍．
解答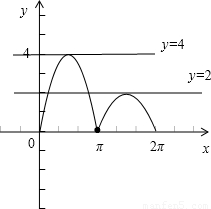：解：因為函數g（x）=3|sinx|+sinx，x∈[0，2π]，
所以當x∈[0，π]時，sinx≥0，函數f（x）=4sinx≥0．
當x∈[π，2π]時，sinx≤0，函數f（x）=-2sinx≥0．
所以g（x）=，
所以根據正弦函數的圖象可得函數g（x）的圖象，如圖所示：
因為函數y=3|sinx|+sinx-k在[0，2π]上有且僅有兩個零點，
即等價于函數與直線y=k有且僅有兩個不同的交點，
所以結合圖象可得：2＜k＜4．
故答案為 （2，4）．
點評：本題主要考查正弦函數的圖象與有關性質，以及考查分類討論、數形結合、轉化化歸的思想方法，考查學生的分析問題解決問題的能力，此題屬于中檔題．