
分析 (1)根據拋物線的焦半徑公式,求得FD的中點坐標,則$\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$=3+2$\sqrt{2}$,即可求得p的值,求得拋物線方程;
(2)設直線AB的方程,代入 拋物線方程,由向量平行即韋達定理,即可求得P點坐標,則△EPB為等腰直角三角形,則kAP=1,由直線的斜率公式可得:y1-y2=4,兩邊平方(y1+y2)2-4y1y2=16,m2=1-x0,x0<1,則d=$\frac{2{x}_{0}}{\sqrt{2-{x}_{0}}}$,根據函數的單調性即可求得點P到直線AB的距離d的取值范圍.
解答 解:(1)由題意可知F($\frac{p}{2}$,0),丨FA丨=3+2$\sqrt{2}$+$\frac{p}{2}$,丨FD丨=$\sqrt{2}$丨FA丨=3$\sqrt{2}$+4+$\frac{\sqrt{2}p}{2}$,
則D(3$\sqrt{2}$+4+$\frac{\sqrt{2}p}{2}$+$\frac{p}{2}$,0),FD的中點坐標($\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$,0),
則$\frac{3\sqrt{2}}{2}$+2+$\frac{(2+\sqrt{2})p}{4}$=3+2$\sqrt{2}$,解得:p=2,
∴拋物線C:y2=4x;
(2)由題意設AB的方程x=my+x0,(m≠0),A(x1,y1),B(x2,y2),E(x2,-y2),
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+{x}_{0}}\end{array}\right.$,消去x,整理得:y2-4my-4=0,
由x0≥$\frac{1}{2}$,△=16m2+16x0>0,
y1+y2=4m,y1y2=-4x0,
設P(xP,0),則$\overrightarrow{PE}$=(x2-xP,-y2),$\overrightarrow{PA}$=(x1-xP,y1),
由$\overrightarrow{PE}$∥$\overrightarrow{PA}$,則(x2-xP)y1+y2(x1-xP)=0,即x2y1+y2x1=(y1+y2)xP=$\frac{{y}_{2}^{2}{y}_{1}+{y}_{1}^{2}{y}_{2}}{4}$=$\frac{{y}_{1}{y}_{2}({y}_{1}+{y}_{2})}{4}$,顯然y1+y2=4m≠0,
∴xP=$\frac{{y}_{1}{y}_{2}}{4}$=-x0,即P(-x0,0),
由題意可知△EPB為等腰直角三角形,
則kAP=1,即$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$=1,則$\frac{{y}_{1}+{y}_{2}}{\frac{1}{4}({y}_{1}^{2}-{y}_{2}^{2})}$=1,則y1-y2=4,
∴(y1+y2)2-4y1y2=16,即16m2+16x0=16,則m2=1-x0,x0<1,
由x0≥$\frac{1}{2}$,則$\frac{1}{2}$≤x0<1,d=$\frac{丨-{x}_{0}-{x}_{0}丨}{\sqrt{1+{m}^{2}}}$=$\frac{2{x}_{0}}{\sqrt{1+{m}^{2}}}$=$\frac{2{x}_{0}}{\sqrt{2-{x}_{0}}}$,
令$\sqrt{2-{x}_{0}}$=t∈(1,$\frac{\sqrt{6}}{2}$],則x0=2-t2,d=$\frac{2(2-{t}^{2})}{t}$=$\frac{4}{t}$-2t,
則f(t)=$\frac{4}{t}$-2t,在(1,$\frac{\sqrt{6}}{2}$]上是減函數,
∴d∈[$\frac{\sqrt{6}}{3}$,2).
點評 本題考查拋物線的性質,直線與拋物線的位置關系,考查向量平行,函數單調性與拋物線的應用,考查計算能力,屬于中檔題.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1>0 | ||
| C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
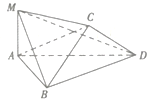 如圖,將邊長為2的正方形ABCD沿對角線BD折疊,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$
如圖,將邊長為2的正方形ABCD沿對角線BD折疊,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM=$\sqrt{2}$查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
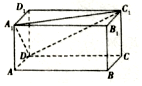 在長方體ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,點E在棱AB上移動.
在長方體ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,點E在棱AB上移動.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com