Question

在半徑為2的圓中隨機地撒一把豆子，則豆子落在原內接正方形ABCD中的概率等于    ．

Answer 1

【答案】分析：在這個圓面上隨意拋一粒豆子，落在圓內每一個地方是均等的，因此計算出正方形和圓的面積，利用幾何概率的計算方法解答即可．
解答：解：⊙O的半徑為2，⊙O的面積為4π；
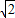
正方形的邊長為：AD=CD==2，面積為8；
因為豆子落在圓內每一個地方是均等的，
所以P（豆子落在正方形ABCD內）==．
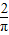
故答案為：．
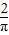
點評：幾何概型的概率估算公式中的“幾何度量”，可以為線段長度、面積、體積等，而且這個“幾何度量”只與“大小”有關，而與形狀和位置無關．解決的步驟均為：求出滿足條件A的基本事件對應的“幾何度量”N（A），再求出總的基本事件對應的“幾何度量”N，最后根據P=N（A）/N求解．