一束光線從點A(-2,1)出發經x軸反射到圓C:(x-2)2+(y-2)2=1上,光線的最短路程是 .
【答案】
分析:由圓C的方程找出圓心C的坐標及圓的半徑r,找出C關于x軸的對稱點C′,連接AC′,利用兩點間的距離公式求出|AC′|的長,用|AC′|的長減去圓的半徑,即可得到光線的最短路程.
解答:解:根據題意畫出圖形,如圖所示:
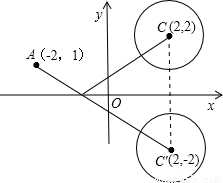
作出圓心C關于x的對稱點C′,連接AC′,
由圓C:(x-2)
2+(y-2)
2=1,得到圓心C坐標為(2,2),圓的半徑r=1,
可得C′的坐標為(2,-2),又A(-2,1),
∴|AC′|=
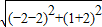
=5,
則光線的最短路程是|AC′|-r=5-1=4.
故答案為:4
點評:此題考查了對稱的性質,兩點間的距離公式,以及圓的標準方程,利用了數形結合的思想,解題的思路為根據題意畫出圖形,作出圓關于x軸的對稱圖形,利用兩點之間線段最短可得出光線的最短距離.


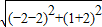 =5,
=5,
