
已知數(shù)列 ,
,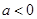 滿足
滿足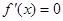 ,
,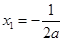 ,
,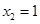 ,
,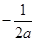 .
.
(1)求證:數(shù)列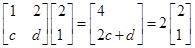 是等差數(shù)列,并求數(shù)列
是等差數(shù)列,并求數(shù)列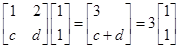 的通項公式;
的通項公式;
(2)設數(shù)列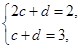 滿足
滿足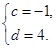 ,對于任意給定的正整數(shù)
,對于任意給定的正整數(shù)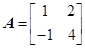 ,是否存在正整數(shù)
,是否存在正整數(shù)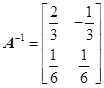 ,
,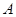 (
( ),使得
),使得 ,
, ,
, 成等差數(shù)列?若存在,試用
成等差數(shù)列?若存在,試用 表示
表示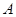 ,
, ;若不存在,說明理由.
;若不存在,說明理由.
(1)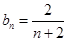 ,(2)當
,(2)當 時,不存在
時,不存在 ,
,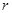 滿足題設條件;當
滿足題設條件;當 時,存在
時,存在 ,
, ,滿足題設條件.
,滿足題設條件.
解析試題分析:(1)求證數(shù)列 是等差數(shù)列,就是確定
是等差數(shù)列,就是確定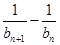 為一個常數(shù).因此首先得到關于
為一個常數(shù).因此首先得到關于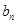 與
與 的關系式,因為
的關系式,因為 ,所以
,所以 ,則
,則 ,然后按提示,將所求關系式進行變形,即取倒數(shù),得:
,然后按提示,將所求關系式進行變形,即取倒數(shù),得: ,又
,又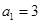 ,所以
,所以 ,故
,故 是首項為
是首項為 ,公差為
,公差為 的等差數(shù)列,即
的等差數(shù)列,即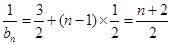 ,所以
,所以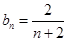 .(2)先明確數(shù)列
.(2)先明確數(shù)列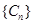 ,由(1)得
,由(1)得 ,所以
,所以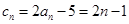 ,然后假設存在,得一等量關系:若
,然后假設存在,得一等量關系:若 ,
, ,
, 成等差數(shù)列,則
成等差數(shù)列,則 ,如何變形,是解題的關鍵,這直接影響解題方向.題中暗示,用p表示,所以由
,如何變形,是解題的關鍵,這直接影響解題方向.題中暗示,用p表示,所以由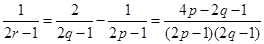 得:
得: .令
.令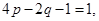 得
得 ,因為要
,因為要 ,所以分情況討論,當
,所以分情況討論,當 時,
時,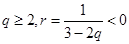 ,
, ,
, ,
, 成等差數(shù)列不成立.當
成等差數(shù)列不成立.當 時,
時, ,
, ,即
,即 .
.
試題解析:(1)因為 ,所以
,所以 ,
,
則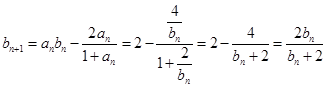 , 2分
, 2分
所以 ,
,
又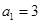 ,所以
,所以 ,故
,故 是首項為
是首項為 ,公差為
,公差為 的等差數(shù)列, 4分
的等差數(shù)列, 4分
即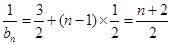 ,所以
,所以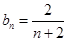 . 6分
. 6分
(2)由(1)知 ,所以
,所以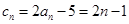 ,
,
①當 時,
時,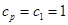 ,
,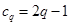 ,
,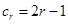 ,
,
若 ,
, ,
, 成等差數(shù)列,則
成等差數(shù)列,則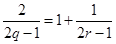 (
( ),
),
因為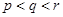 ,所以
,所以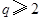 ,
, ,
,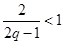 ,
, ,
,
所以( )不成立.
)不成立.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數(shù)學 來源: 題型:解答題
(12分)(2011•重慶)設實數(shù)數(shù)列{an}的前n項和Sn滿足Sn+1=an+1Sn(n∈N*).
(Ⅰ)若a1,S2,﹣2a2成等比數(shù)列,求S2和a3.
(Ⅱ)求證:對k≥3有0≤ak≤ .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(2013•湖北)已知等比數(shù)列{an}滿足:|a2﹣a3|=10,a1a2a3=125.
(1)求數(shù)列{an}的通項公式;
(2)是否存在正整數(shù)m,使得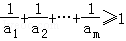 ?若存在,求m的最小值;若不存在,說明理由.
?若存在,求m的最小值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
在等比數(shù)列
(1)求數(shù)列{an}的通項公式;
(2)求數(shù)列{an}的前5項的和 ;
;
(3)若 ,求Tn的最大值及此時n的值.
,求Tn的最大值及此時n的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
學校餐廳每天供應500名學生用餐,每星期一有A, B兩種菜可供選擇。調(diào)查表明,凡是在這星期一選A菜的,下星期一會有 改選B菜;而選B菜的,下星期一會有
改選B菜;而選B菜的,下星期一會有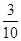 改選A菜。用
改選A菜。用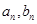 分別表示第
分別表示第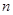 個星期選A的人數(shù)和選B的人數(shù).
個星期選A的人數(shù)和選B的人數(shù).
⑴試用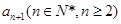 表示
表示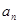 ,判斷數(shù)列
,判斷數(shù)列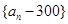 是否成等比數(shù)列并說明理由;
是否成等比數(shù)列并說明理由;
⑵若第一個星期一選A種菜的有200人,那么第10個星期一選A種菜的大約有多少人?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
若函數(shù)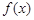 滿足:集合
滿足:集合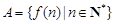 中至少存在三個不同的數(shù)構成等比數(shù)列,則稱函數(shù)
中至少存在三個不同的數(shù)構成等比數(shù)列,則稱函數(shù)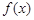 是等比源函數(shù).
是等比源函數(shù).
(1)判斷下列函數(shù):①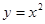 ;②
;②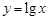 中,哪些是等比源函數(shù)?(不需證明)
中,哪些是等比源函數(shù)?(不需證明)
(2)證明:函數(shù)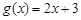 是等比源函數(shù);
是等比源函數(shù);
(3)判斷函數(shù)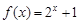 是否為等比源函數(shù),并證明你的結論.
是否為等比源函數(shù),并證明你的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知各項均為正數(shù)的數(shù)列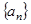 前n項和為
前n項和為 ,首項為
,首項為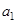 ,且
,且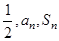 等差數(shù)列。
等差數(shù)列。
(1)求數(shù)列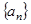 的通項公式;
的通項公式;
(2)若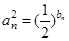 ,設
,設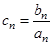 ,求數(shù)列
,求數(shù)列 的前n項和
的前n項和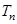 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設數(shù)列{an}前n項和為Sn,數(shù)列{Sn}的前n項和為Tn,滿足Tn=2Sn-n2,n∈N*.
(1)求a1的值.
(2)求數(shù)列{an}的通項公式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com