
【題目】隨著“互聯網+交通”模式的迅猛發展,“共享自行車”在很多城市相繼出現。某運營公司為了了解某地區用戶對其所提供的服務的滿意度,隨機調查了40個用戶,得到用戶的滿意度評分如下:
用戶編號 | 評分 | 用戶編號 | 評分 | 用戶編號 | 評分 | 用戶編號 | 評分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系統抽樣法從40名用戶中抽取容量為10的樣本,且在第一分段里隨機抽到的評分數據為92.
(1)請你列出抽到的10個樣本的評分數據;
(2)計算所抽到的10個樣本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)條件下,若用戶的滿意度評分在![]() 之間,則滿意度等級為“
之間,則滿意度等級為“![]() 級”。試應用樣本估計總體的思想,根據所抽到的10個樣本,估計該地區滿意度等級為“
級”。試應用樣本估計總體的思想,根據所抽到的10個樣本,估計該地區滿意度等級為“![]() 級”的用戶所占的百分比是多少?
級”的用戶所占的百分比是多少?
(參考數據:![]() )
)
【答案】(1)見解析;(2)均值![]() ,方差
,方差![]() (3)
(3)![]()
【解析】
(1)根據題意,由表格分析可得通過系統抽樣分別抽取編號,據此可得樣本的評分數據;
(2)根據題意,由平均數和方差公式計算可得答案;
(3)根據題意,分析評分在![]() ,即(77.26,88.74)之間的人數,進而計算進而可得答案.
,即(77.26,88.74)之間的人數,進而計算進而可得答案.
(1)通過系統抽樣抽取的樣本編號為:4,8,12,16,20,24,28,32,36,40
則樣本的評分數據為:92,84,86,78,89,74,83,78,77,89.
(2)由(1)中的樣本評分數據可得
![]() ,
,
則有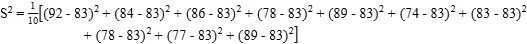
![]()
所以均值![]() ,方差
,方差![]() .
.
(3)由題意知評分在![]() 即
即![]() 之間滿意度等級為“A級”,
之間滿意度等級為“A級”,
由(1)中容量為10的樣本評分在![]() 之間有5人,
之間有5人,
則該地區滿意度等級為“A級”的用戶所占的百分比約為![]()


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 上恰有2個點到
上恰有2個點到![]() 的距離等于
的距離等于![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在凸四邊形ABCD中,M為邊AB的中點,且MC=MD.分別過點C、D作邊BC、AD的垂線,設兩條垂線的交點為P.過點P作![]() 與Q.求證:
與Q.求證:![]() .
.
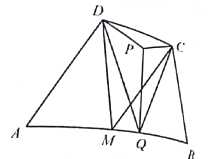
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() ,定義橢圓
,定義橢圓![]() 的“相關圓”方程為
的“相關圓”方程為![]() .若拋物線
.若拋物線![]() 的焦點與橢圓
的焦點與橢圓![]() 的一個焦點重合,且橢圓
的一個焦點重合,且橢圓![]() 短軸的一個端點和其兩個焦點構成直角三角形.
短軸的一個端點和其兩個焦點構成直角三角形.
(1)求橢圓![]() 的方程和“相關圓”
的方程和“相關圓”![]() 的方程;
的方程;
(2)過“相關圓”![]() 上任意一點
上任意一點![]() 的直線l:
的直線l:![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.O為坐標原點,若
兩點.O為坐標原點,若![]() ,證明原點O到直線
,證明原點O到直線![]() 的距離是定值,并求
的距離是定值,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線的一條弦的中點作平行于拋物線對稱軸的平行線(或與對稱軸重合),交拋物線于一點,稱以該點及弦的端點為頂點的三角形為這條弦的阿基米德三角形(簡稱阿氏三角形).
現有拋物線![]() :
:![]() ,直線
,直線![]() :
:![]() (其中
(其中![]() ,
,![]() ,
,![]() 是常數,且
是常數,且![]() ),直線
),直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,設弦
兩點,設弦![]() 的阿氏三角形是
的阿氏三角形是![]() .
.

(1)指出拋物線![]() 的焦點坐標和準線方程;
的焦點坐標和準線方程;
(2)求![]() 的面積(用
的面積(用![]() ,
,![]() ,
,![]() 表示);
表示);
(3)稱![]() 的阿氏
的阿氏![]() 為一階的;
為一階的;![]() 、
、![]() 的阿氏
的阿氏![]() 、
、![]() 為二階的;
為二階的;![]() 、
、![]() 、
、![]() 、
、![]() 的阿氏三角形為三階的;……,由此進行下去,記所有的
的阿氏三角形為三階的;……,由此進行下去,記所有的![]() 階阿氏三角形的面積之和為
階阿氏三角形的面積之和為![]() ,探索
,探索![]() 與
與![]() 之間的關系,并求
之間的關系,并求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大學先修課程,是在高中開設的具有大學水平的課程,旨在讓學有余力的高中生早接受大學思維方式、學習方法的訓練,為大學學習乃至未來的職業生涯做好準備.某高中成功開設大學先修課程已有兩年,共有250人參與學習先修課程,這兩年學習先修課程的學生都參加了高校的自主招生考試(滿分100分),結果如下表所示:
分數 |
|
|
|
|
|
人數 | 25 | 50 | 100 | 50 | 25 |
參加自主招生獲得通過的概率 | 0.9 | 0.8 | 0.6 | 0.4 | 0.3 |
(Ⅰ)這兩年學校共培養出優等生150人,根據下圖等高條形圖,填寫相應列聯表,并根據列聯表檢驗能否在犯錯的概率不超過0.01的前提下認為學習先修課程與優等生有關系?
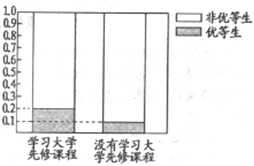
優等生 | 非優等生 | 總計 | |
學習大學先修課程 | 250 | ||
沒有學習大學先修課程 | |||
總計 | 150 |
(Ⅱ)已知今年全校有150名學生報名學習大學選項課程,并都參加了高校的自主招生考試,以前兩年參加大學先修課程學習成績的頻率作為今年參加大學先修課程學習成績的概率.
(ⅰ)在今年參與大學先修課程學習的學生中任取一人,求他獲得高校自主招生通過的概率;
(ⅱ)某班有4名學生參加了大學先修課程的學習,設獲得高校自主招生通過的人數為![]() ,求
,求![]() 的分布列,試估計今年全校參加大學先修課程學習的學生獲得高校自主招生通過的人數.
的分布列,試估計今年全校參加大學先修課程學習的學生獲得高校自主招生通過的人數.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(題文)已知![]() 是直線
是直線![]() 上的動點,點
上的動點,點![]() 的坐標是
的坐標是![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 垂直,并且
垂直,并且![]() 與線段
與線段![]() 的垂直平分線相交于點
的垂直平分線相交于點![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設曲線![]() 上的動點
上的動點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的另一個交點為
的另一個交點為![]() (
(![]() 與
與![]() 不重合),是否存在一個定點
不重合),是否存在一個定點![]() ,使得
,使得![]() 三點共線?若存在,求出點
三點共線?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com