
【題目】已知a∈R,若關于x的方程x2+x+|a﹣ ![]() |+|a|=0有實根,則a的取值范圍是
|+|a|=0有實根,則a的取值范圍是
【答案】![]()
【解析】解:x2+x+|a﹣ ![]() |+|a|=0即|a﹣
|+|a|=0即|a﹣ ![]() |+|a|=﹣(x2+x),
|+|a|=﹣(x2+x),
令y=﹣(x2+x),
分析可得,y≤ ![]() ,
,
若方程x2+x+|a﹣ ![]() |+|a|=0有實根,則必有|a﹣
|+|a|=0有實根,則必有|a﹣ ![]() |+|a|≤
|+|a|≤ ![]() ,
,
而|a﹣ ![]() |+|a|≥
|+|a|≥ ![]() ,當且僅當0≤a≤
,當且僅當0≤a≤ ![]() 時,有|a﹣
時,有|a﹣ ![]() |+|a|=
|+|a|= ![]() ,
,
故且僅當0≤a≤ ![]() 時,有|a﹣
時,有|a﹣ ![]() |+|a|=﹣(x2+x)成立,即x2+x+|a﹣
|+|a|=﹣(x2+x)成立,即x2+x+|a﹣ ![]() |+|a|=0有實根,
|+|a|=0有實根,
可得實數a的取值范圍為 ![]() ,
,
所以答案是: ![]() .
.
【考點精析】解答此題的關鍵在于理解絕對值不等式的解法的相關知識,掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號.


科目:高中數學 來源: 題型:
【題目】某玩具所需成本費用為P元,且P=1 000+5x+![]() x2,而每套售出的價格為Q元,其中Q(x)=a+
x2,而每套售出的價格為Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)問:玩具廠生產多少套時,使得每套所需成本費用最少?
(2)若生產出的玩具能全部售出,且當產量為150套時利潤最大,此時每套價格為30元,求a,b的值.(利潤=銷售收入-成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
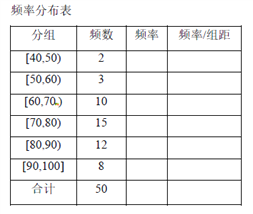
【題目】某校高三年級進行了一次學業水平測試,用系統抽樣的方法抽取了50名學生的數學成績,準備進行分析和研究.經統計,成績的分組及各組的頻數如下: ![]() ,2;
,2; ![]() ,3;
,3; ![]() ,10;
,10; ![]()
15; ![]() ,12;
,12; ![]() ,8.
,8.
(1)完成樣本的頻率分布表,畫出頻率分布直方圖;
(2)估計成績在85分以下的學生比例;
(3)請你根據以上信息去估計樣本的眾數、中位數、平均數(精確到0.01).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=2 ![]() cos2x﹣2sinxcosx﹣
cos2x﹣2sinxcosx﹣ ![]() 的圖象向左平移t(t>0)個單位,所得圖象對應的函數為奇函數,則t的最小值為( )
的圖象向左平移t(t>0)個單位,所得圖象對應的函數為奇函數,則t的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為角A,B,C所對的三邊,a2﹣(b﹣c)2=bc,
(1)求角A;
(2)若BC=2 ![]() ,角B等于x,周長為y,求函數y=f(x)的取值范圍.
,角B等于x,周長為y,求函數y=f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正三棱錐A﹣BCD的外接球半徑R= ![]() ,P,Q分別是AB,BC上的點,且滿足
,P,Q分別是AB,BC上的點,且滿足 ![]() =
= ![]() =5,DP⊥PQ,則該正三棱錐的高為( )
=5,DP⊥PQ,則該正三棱錐的高為( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A,B,C成等差數列是(b+a﹣c)(b﹣a+c)=ac的( )
A.充分但不必要條件
B.必要但不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com