設關于x的函數y=-2sin2x-2asinx-(2a+1)的最大值為f(a)
(1)求f(a)的表達式
(2)確定使f(a)=5的a的值,并對此時的a,求y的最小值.
【答案】
分析:(1)由已知中函數y=-2sin
2x-2asinx-(2a+1)的最大值為f(a),利用換元法我們令t=sinx,(-1≤t≤1),結合二次函數在定區間上的最值問題的處理方法,即可得到f(a)的表達式.
(2)由(1)中f(a)的表達式,我們分別討論使f(a)=5的a的值,并根據分類標準進行取舍,最后綜合討論結果即可得到f(a)=5的a的值,進而求出對應的y的最小值.
解答:解:(1)y=-2sin
2x-2asinx-(2a+1)=-2(sinx+
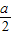
)
2+
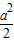
-(2a+1)
令t=sinx,(-1≤t≤1)
當-
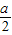
<-1,即a>2時,
f(a)=-3
當-1≤-
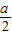
≤1,即-2≤a≤2時,
f(a)=
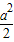
-2a-1
當-
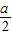
>1,即a<-2時
f(a)=-4a-3
∴f(a)=

(2)當a>2時,f(a)=-3≠5
當-2≤a≤2時,f(a)=
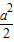
-2a-1=5
解得a=-2,或a=6(舍去)
當a<-2時,f(a)=-4a-3=5
則a=-2(舍去)
綜上所述a=-2
此時,y=-2(t-1)
2+5,(-1≤t≤1)
當t=-1時,y取最小值-3
點評:本題考查的知識點是三角函數的最值,其中利用換元法,將問題轉化為二次函數在定區間上的最值問題,是解答本題的關鍵.

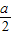 )2+
)2+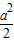 -(2a+1)
-(2a+1)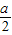 <-1,即a>2時,
<-1,即a>2時,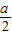 ≤1,即-2≤a≤2時,
≤1,即-2≤a≤2時,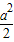 -2a-1
-2a-1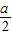 >1,即a<-2時
>1,即a<-2時
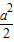 -2a-1=5
-2a-1=5
