
已知函數 .
.
(1)若對于區間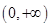 內的任意
內的任意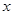 ,總有
,總有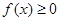 成立,求實數
成立,求實數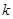 的取值范圍;
的取值范圍;
(2)若函數 在區間
在區間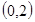 內有兩個不同的零點
內有兩個不同的零點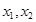 ,求:
,求:
①實數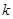 的取值范圍; ②
的取值范圍; ②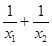 的取值范圍.
的取值范圍.
(1)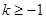 ;(2)
;(2)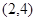 .
.
解析試題分析:(1)分離參數,若對于區間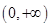 內的任意
內的任意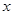 ,總有
,總有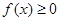 成立,得
成立,得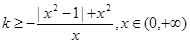 ,再求出
,再求出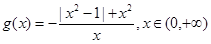 的最大值即可;
的最大值即可;
(2)先去絕對值,當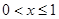 時,方程
時,方程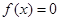 化為
化為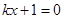 ,
,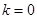 時,無解;
時,無解;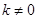 時,
時,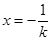 ;
;
當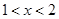 時,方程
時,方程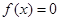 化為
化為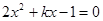 ,
,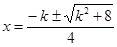 ,而其中
,而其中 ,故
,故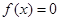 在區間
在區間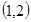 內至多有一解
內至多有一解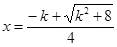 ;
;
綜合ⅰ)ⅱ)可知,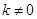 ,且
,且 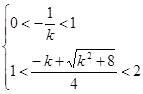 ,得
,得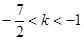 .
.
試題解析:(1)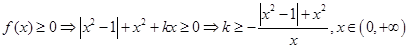 ,
,
記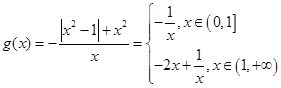 ,易知
,易知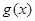 在上
在上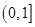 遞增,在
遞增,在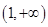 上遞減,
上遞減,
∴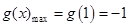 ,∴
,∴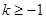 即可 (5分)
即可 (5分)
(2)①ⅰ)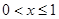 時,方程
時,方程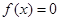 化為
化為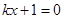 ,
,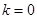 時,無解;
時,無解;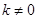 時,
時,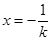 ;
;
ⅱ)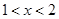 時,方程
時,方程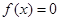 化為
化為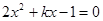 ,
,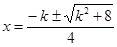 ,而其中
,而其中 ,故
,故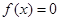 在區間
在區間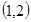 內至多有一解
內至多有一解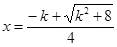 ;
;
綜合ⅰ)ⅱ)可知,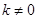 ,且
,且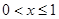 時,方程
時,方程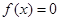 有一解
有一解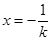 ,故
,故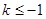 ;
;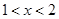 時,方程
時,方程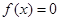 也僅有一解
也僅有一解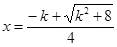 ,令
,令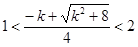 ,得
,得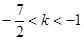 ,所以實數
,所以實數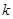 的取值范圍是
的取值范圍是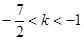 ; (10分)
; (10分)
②方程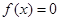 的兩解分別為
的兩解分別為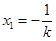 ,
,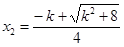 ,
,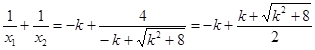
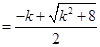
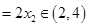 (14分)
(14分)
考點:(1)絕對值,不等式的恒成立問題;(2)函數與方程,函數的零點


科目:高中數學 來源: 題型:解答題
某公司以每噸10萬元的價格銷售某種產品,每年可售出該產品1000噸,若將該產品每噸的價格上漲x%,則每年的銷售數量將減少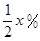 ,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校要建一個面積為450平方米的矩形球場,要求球場的一面利用舊墻,其他各面用鋼筋網圍成,且在矩形一邊的鋼筋網的正中間要留一個3米的進出口(如圖).設矩形的長為 米,鋼筋網的總長度為
米,鋼筋網的總長度為 米.
米.
(1)列出 與
與 的函數關系式,并寫出其定義域;
的函數關系式,并寫出其定義域;
(2)問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
(3)若由于地形限制,該球場的長和寬都不能超過25米,問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若在定義域內存在實數
,若在定義域內存在實數 ,滿足
,滿足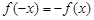 ,則稱
,則稱 為“局部奇函數”.
為“局部奇函數”.
(1)已知函數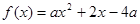
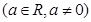 ,試判斷
,試判斷 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)若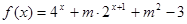 為定義域
為定義域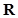 上的“局部奇函數”,求實數m的取值范圍.
上的“局部奇函數”,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
市場營銷人員對過去幾年某商品的價格及銷售數量的關系作數據分析發現有如下規律:該商品的價格每上漲x%(x>0),銷售數量就減少kx%(其中k為正常數).目前該商品定價為每個a元,統計其銷售數量為b個.
(1)當k= 時,該商品的價格上漲多少,才能使銷售的總金額達到最大?
時,該商品的價格上漲多少,才能使銷售的總金額達到最大?
(2)在適當的漲價過程中,求使銷售總金額不斷增加時k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地方政府在某地建一座橋,兩端的橋墩相距m米,此工程只需建兩端橋墩之間的橋面和橋墩(包括兩端的橋墩).經預測,一個橋墩的費用為256萬元,相鄰兩個橋墩之間的距離均為x,且相鄰兩個橋墩之間的橋面工程費用為(1+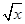 )x萬元,假設所有橋墩都視為點且不考慮其他因素,記工程總費用為y萬元.
)x萬元,假設所有橋墩都視為點且不考慮其他因素,記工程總費用為y萬元.
(1)試寫出y關于x的函數關系式;
(2)當m=1280米時,需要新建多少個橋墩才能使y最小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com