【題目】將高二（1）班的四個同學分到語文、數學、英語三個興趣小組，每個興趣小組至少有一名同學的分配方法有多少種？下列結論正確的有（ ）
A.
B.
C.
D.18
【答案】BC
【解析】
根據題意，有2種解法，
解法1，先將4人分三組，再將分好的三組全排列，由分布計數原理計算可得B正確；
解法2，在3個小組中選出1個，安排2個同學，再將剩下的2人全排列，對應剩下的2個興趣小組，由分布計數原理計算可得C正確；即可得答案；
解：根據題意，
解法1，先將4人三組，有C42種分組方法，再將分好的三組全排列，對應三個興趣小組，有A33種情況，則有C42A33種分配方法，B正確；
解法2，在3個小組中選出1個，安排2個同學，有C31C42種情況，再將剩下的2人全排列，對應剩下的2個興趣小組，有A22種情況，則有C31C42A22種分配方法，C正確；
故選：BC.
小學教材完全解讀系列答案科目：高中數學 來源： 題型：
【題目】某醫療器械公司在全國共有
個銷售點，總公司每年會根據每個銷售點的年銷量進行評價分析.規定每個銷售點的年銷售任務為一萬四千臺器械.根據這個銷售點的年銷量繪制出如下的頻率分布直方圖.
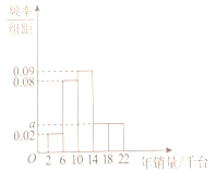
（1）完成年銷售任務的銷售點有多少個？
（2）若用分層抽樣的方法從這個銷售點中抽取容量為
的樣本，求該五組
，
，
，
，
，（單位：千臺）中每組分別應抽取的銷售點數量.
（3）在（2）的條件下，從前兩組，中的銷售點隨機選取
個，記這個銷售點在中的個數為
，求的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點
，
，且橢圓過點
，
，且
是橢圓上位于第一象限的點，且
的面積
.
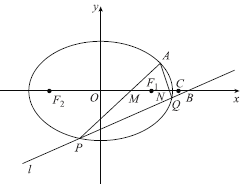
（1）求點的坐標；
（2）過點
的直線
與橢圓
相交于點
，
，直線
，
與
軸相交于
，
兩點，點
，則
是否為定值，如果是定值，求出這個定值，如果不是請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】 據觀測統計，某濕地公園某種珍稀鳥類的現有個數約
只，并以平均每年
的速度增加．
(1)求兩年后這種珍稀鳥類的大約個數；
(2)寫出
（珍稀鳥類的個數）關于
（經過的年數）的函數關系式；
(3)約經過多少年以后，這種鳥類的個數達到現有個數的
倍或以上？（結果為整數）(參考數據：
，
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，n∈N*.
（1）設f(x)＝a0+a1x+a2x2+…+anxn，
①求a0+a1+a2+…+an；
②若在a0，a1，a2，…，an中，唯一的最大的數是a4，試求n的值；
（2）設f(x)＝b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n，求
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
